



Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости
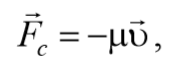
Формула 5.6.1
где μ − постоянная, называемая коэффициентом сопротивления.
Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид
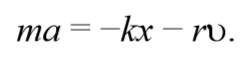
Формула 5.6.2
Учитывая , что a=$$d^2x\over dt^2$$, а υ=$$dx\over dt$$ и разделив на массу m, получим
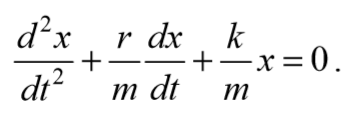
Формула 5.6.3
Применив обозначения $${k\over m} = ω_0{^2}$$, $${μ\over m} = 2β$$ и $${F_0\over m} = f_0$$ получим
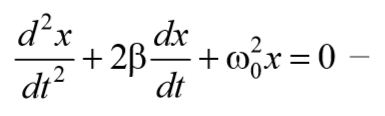
Формула 5.6.4
дифференциальное уравнение затухающих колебаний. Отметим, что ω0 представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой.
Для решения уравнения (5.6.4) сделаем подстановку
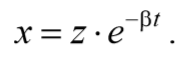
Формула 5.6.5
Проведем замену переменных
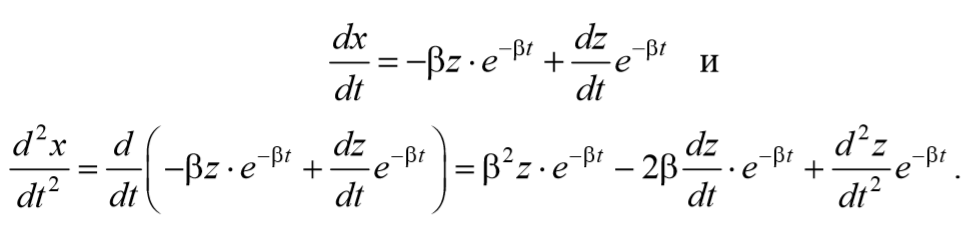
Формула 5.6.6
Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)
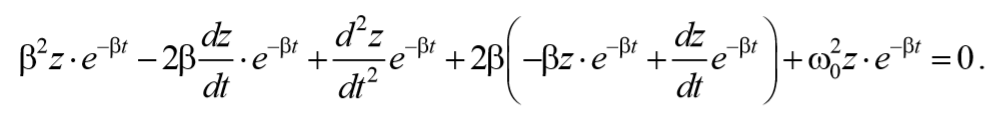
Формула 5.6.7
Преобразуем , сократив на e-βt
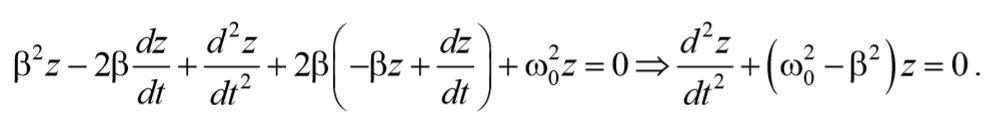
Формула 5.6.8
Рассмотрим случай, когда сопротивление среды настолько мало, что ω02-β2>0 есть величина положи мы можем ввести тельная, и обозначение ω02-β2=ω2, после чего уравнение (5.6.8) примает вид
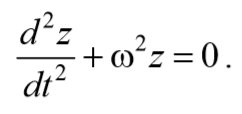
Формула 5.6.9
В случае большого сопротивления среды ω02-β2<0, движение становится непериодическим.
Решение уравнения (5.6.8) можно записать в виде
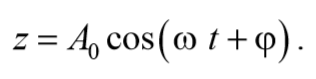
Формула 5.6.10
Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)
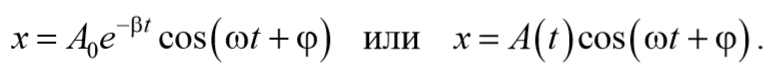
Формула 5.6.11
В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой
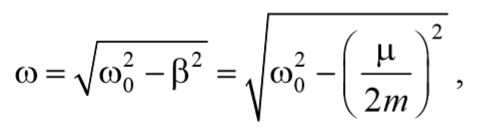
Формула 5.6.12
периодом
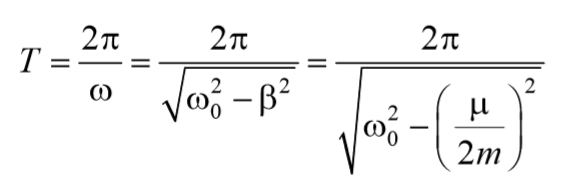
Формула 5.6.13
и амплитудой, изменяющейся по закону
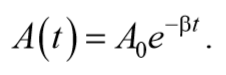
Формула 5.6.14
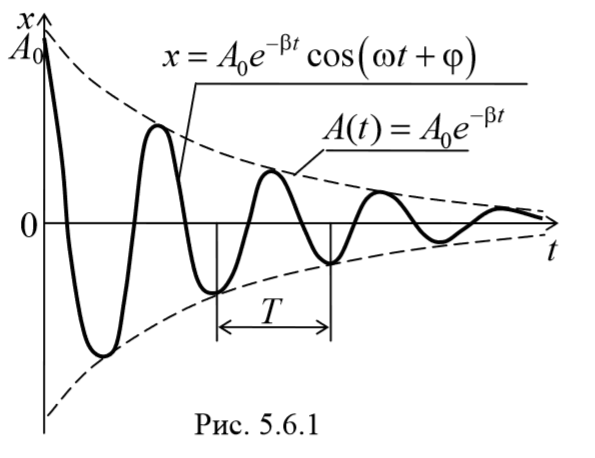
На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t), причем величина A0 представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A0 и также от начальной фазы φ, т.е. x0=A0cosφ.
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
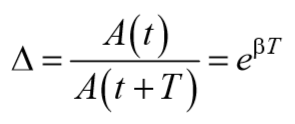
Формула 5.7.1
и называется декрементом затухания.
Для характеристики системы обычно используется колебательной логарифмический декремент затухания, т.е. логарифм декремента затухания
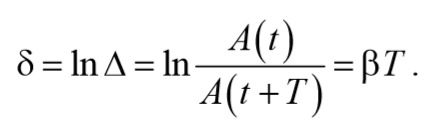
Формула 5.7.2
Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β={μ\over 2m}$$.
Найдем время, называемое временем релаксации τ, за которое амплитуда уменьшается в e раз
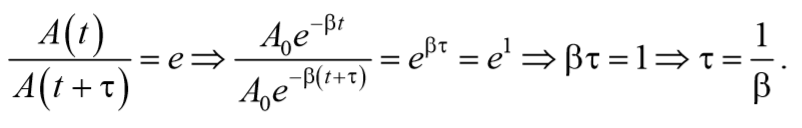
Формула 5.7.3
Следовательно,
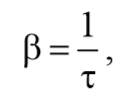
Формула 5.7.4
т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.
За время релаксации τ система успевает совершить $$N_e={τ\over T}$$ колебаний
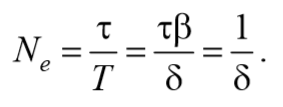
Формула 5.7.5
Следовательно, $$δ={1\over N_e}$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.
Для характеристики колебательной системы используется величина
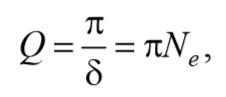
Формула 5.7.6
которая называется добротностью колебательной системы.
Величина Q, пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.
До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F0cosωt. Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями. В этом случае уравнение второго закона Ньютона имеет вид
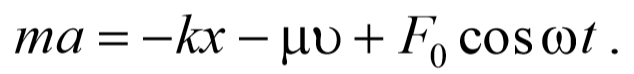
Формула 5.8.1
Учитывая , что a=$$d^2x\over dt^2$$, а υ=$$dx\over dt$$ и разделив на массу m, получим
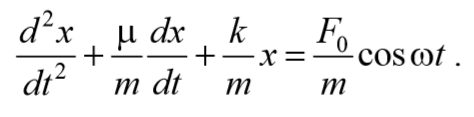
Формула 5.8.2
Применив обозначения $${k\over m} = ω_0{^2}$$, $${μ\over m} = 2β$$ и $${F_0\over m} = f_0$$ получим
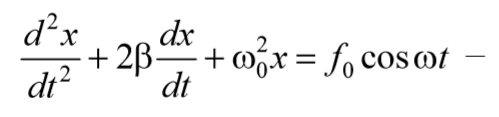
Формула 5.8.3
дифференциальное уравнение вынужденных колебаний.
Будем искать решение уравнения (5.8.3) в виде
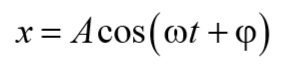
Формула 5.8.4
предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.
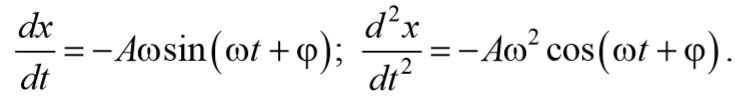
Формула 5.8.5
Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)
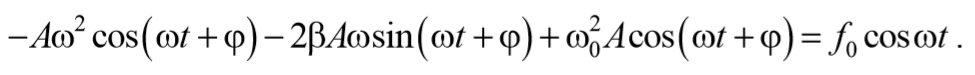
Формула 5.8.6
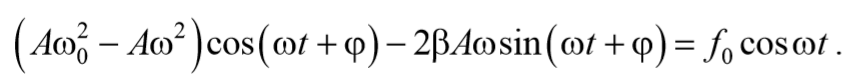
Формула 5.8.7
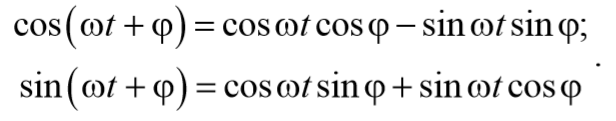
Формула 5.8.8
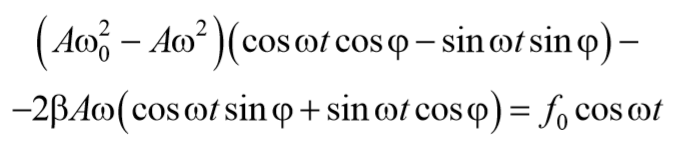
Формула 5.8.9
Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.
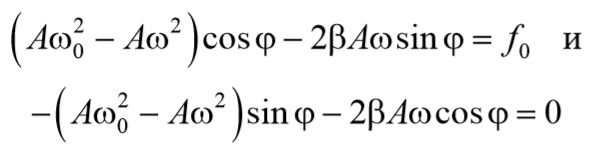
Формула 5.8.10
Из выражения (71) получаем
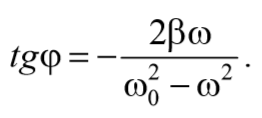
Формула 5.8.11
Возведем в квадрат уравнения (70) и сложим
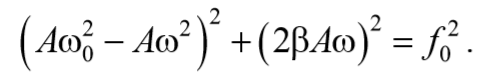
Формула 5.8.12
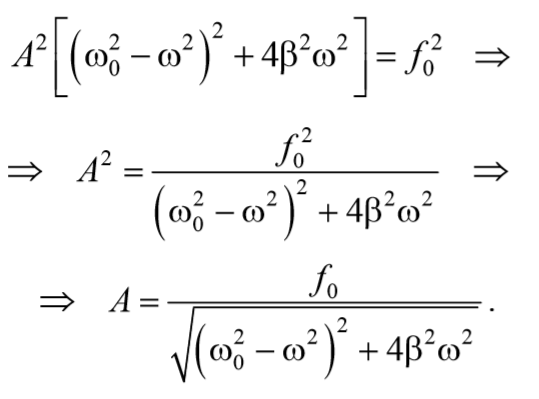
Формула 5.8.13
Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний
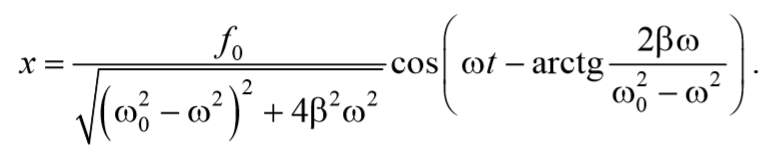
Формула 5.8.14
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом, а соответствующая частота − резонансной частотой.
Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0{^2}-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A={f_0\over \sqrt {(ω_0{^2}-ω^2)^2 + 4β^2ω^2}}$$ (5.8.13) будет минимальным.
Продифференцируем это выражение по ω и приравняем к нулю
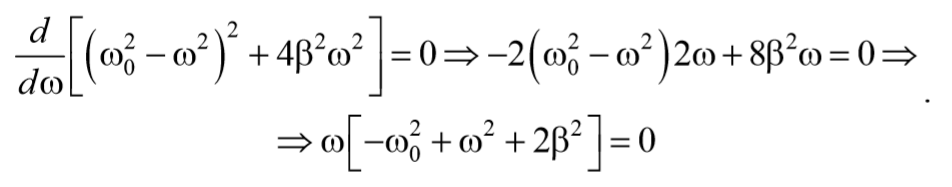
Формула 5.9.1
Полученное уравнение имеет три решения: ω=0 и ω=±$$\sqrt {ω_0{^2}-2β^2}$$. 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота
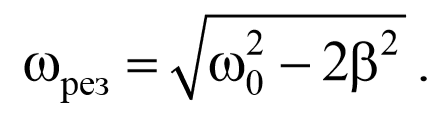
Формула 5.9.2
Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе
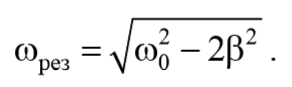
Формула 5.9.3
Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0), совпадала бы с собственной частотой колебаний системы ω0
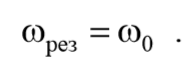
Формула 5.9.4
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β, тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β, называется резонансными кривыми.
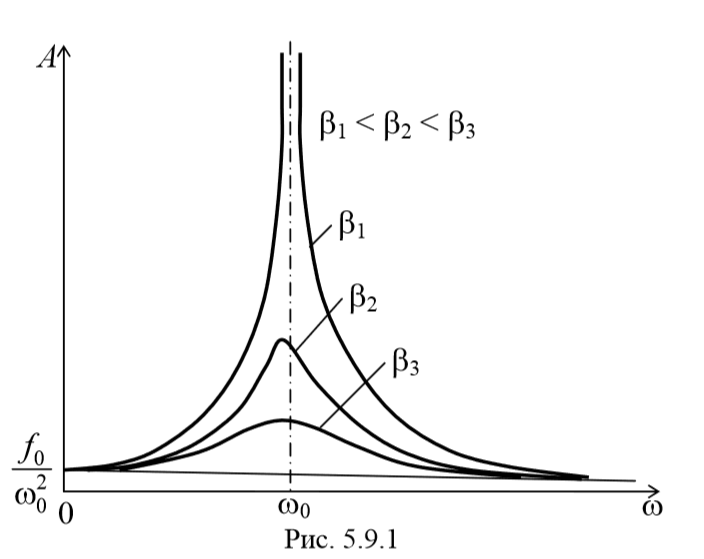
При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f0ω02. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F0
При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.
Наконец, отметим, что чем меньше β, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β<<ω0) амплитуда при резонансе приближенно равна Apes≈f0/2βω0. Разделим это выражение на смещение x0 из положения равновесия под действием постоянной силы F0, равное x0=f0/ωp2. В результате получим
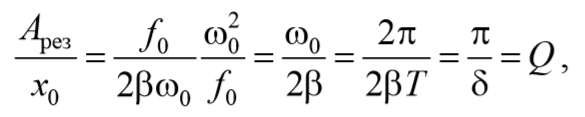
Формула 5.9.5
где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).
Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.