Основные понятия, формулы, законы и уравнения

Кинематика материальной точки и твердого тела

  1. Задание движения материальной точки в векторной форме:
    1. кинематический закон движения:

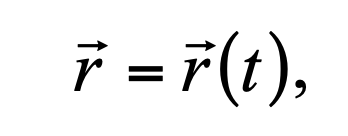
      Формула 1.1

      где r − радиус-вектор движущейся материальной точки;

    2. вектор мгновенной скорости:

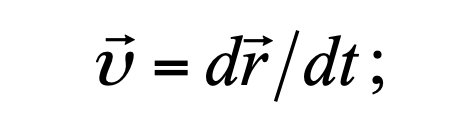
      Формула 1.2

    3. вектор мгновенного ускорения:

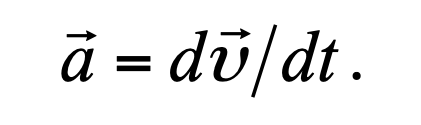
      Формула 1.3

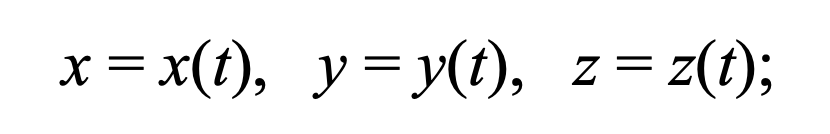
  2. Задание движения материальной точки в координатной форме:
    1. закон движения:

      Формула 1.4

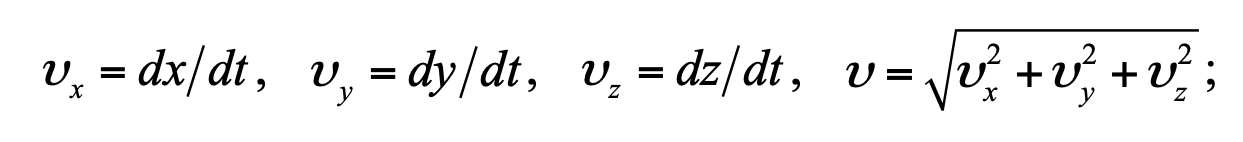
    2. проекции и модуль вектора мгновенной скорости:

      Формула 1.5

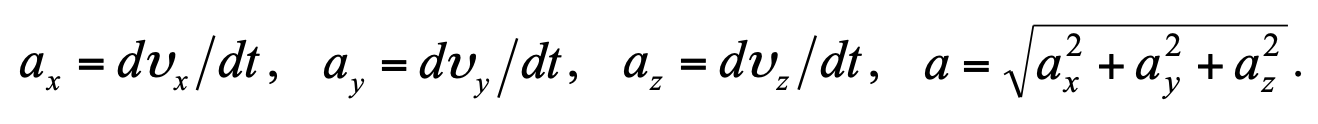
    3. проекции и модуль вектора мгновенного ускорения:

      Формула 1.6

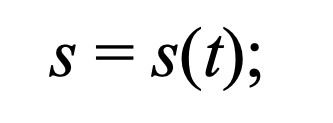
  3. Задание движения материальной точки в естественной форме (s − дуговая координата):
    1. закон движения:

      Формула 1.7

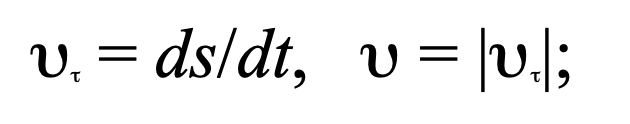
    2. проекция скорости на касательную к траектории точки и модуль скорости:

      Формула 1.8

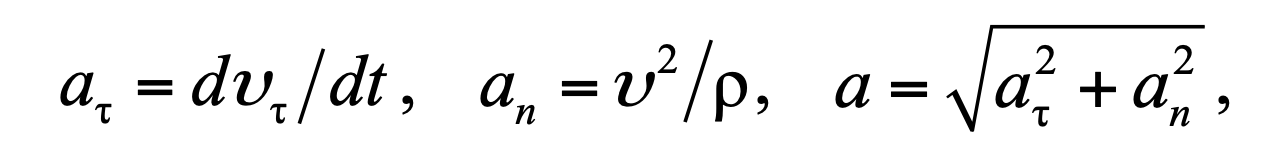
    3. проекции ускорения на касательную и нормаль к траектории точки, а также модуль ускорения:

      Формула 1.9

      где aτ и an − соответственно тангенциальное и нормальное ускорения;

      ρ− радиус кривизны траектории движущейся точки.

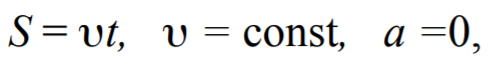
  4. Частные случаи движения материальной точки:
    1. прямолинейное равномерное движение:

      Формула 1.10

      где S – путь, пройденный материальной точкой за время t;
    2. прямолинейное равнопеременное движение:

      Формула 1.11

      где υ0 – начальная скорость материальной точки.

  5. Абсолютно твердое тело – тело, которое не может деформироваться, при всех условиях расстояние между любыми двумя точками этого тела остается постоянным.

    Простейшие виды движения твердого тела – поступательное движение и вращательное движение вокруг неподвижной оси.

    Поступательное движение – движение, при котором любая прямая линия, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению.

    Вращательное движение твердого тела вокруг неподвижной оси движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения, а плоскости этих окружностей перпендикулярны этой оси.

  6. Основными кинематическими параметрами вращательного движения являются угол поворота ϕ, угловая скорость ω и угловое ускорение ε:
    1. закон вращательного движения твердого тела:

      Формула 1.12

    2. угловая скорость:

      Формула 1.13

    3. угловое ускорение:

      Формула 1.14

  7. Уравнения связи между линейными и угловыми кинематическими величинами:

    Уравнения связи 1.15

    где R − кратчайшее расстояние от точки до оси вращения.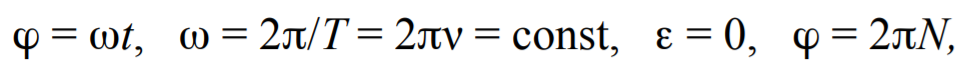
  8. Частные случаи вращательного движения твердого тела:
    1. равномерное вращение твердого тела:

      Формула 1.16

      где T − период вращения тела; ν − частота вращения, т.е. количество оборотов в единицу времени; N − полное количество оборотов;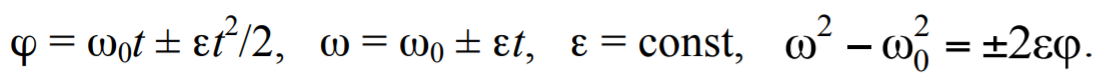
    2. равнопеременное вращение твердого тела:

      Формула 1.17

Динамика материальной точки и абсолютно твердого тела

  1. Инертность тела − это свойство тела сохранять неизменным состояние своего движения или покоя при отсутствии внешних воздействий.
  2. Масса m тела − физическая величина, являющаяся мерой его инерционных и гравитационных свойств.

    Импульс p точки (количество движения) − физическая величина, равная произведению массы точки на ее скорость: .

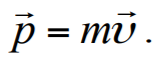
    Формула 1.18

    Сила F − векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.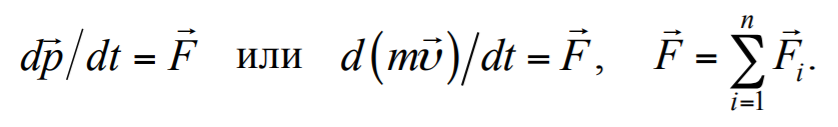
  3. Первый закон Ньютона (закон инерции): существуют такие системы отсчета (инерциальные системы отчета), относительно которых тела сохраняют состояние покоя или равномерного прямолинейного движения, до тех пор, пока силовое воздействие со стороны других тел не изменит их состояние.
  4. Второй закон Ньютона: скорость изменения импульса p материальной точки равна равнодействующей сила F , действующей на эту точку, т.е.

    Формула 1.19

    Если масса точки с течением времени не изменяется (m = const), то

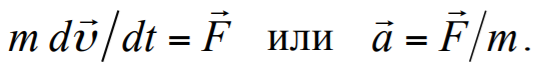
    Формула 1.20

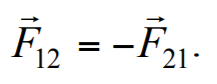
  5. Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, равны по величине, противоположны по направлению и действуют вдоль прямой, которая соединяет эти точки

    Формула 1.21

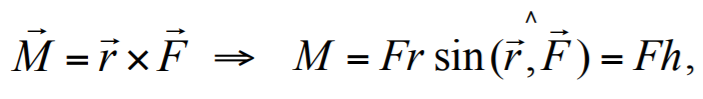
  6. Момент силы F, действующей на тело, относительно центра O:

    Формула 1.22

    где r − радиус-вектор, соединяющий центр O с точкой, к которой приложена сила F;h − плечо силы F: кратчайшее расстояние (длина проведенного перпендикуляра) от центра О до линии действия силы F.

    Момент силы L относительно оси вращения z, проходящей через центр O, равен проекции M на эту ось:

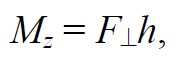
    Формула 1.23

    где F⊥ − составляющая силы, которая перпендикулярна оси; h − плечо этой составляющей силы относительно точки, находящейся на оси z.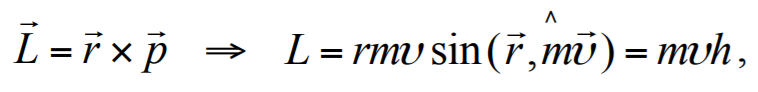
  7. Момент импульса L материальной точки относительно центра O:

    Формула 1.24

    где h − плечо импульса p = m υ материальной точки.
  8. Уравнение моментов для материальной точки: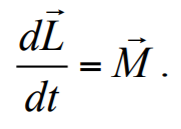

    Формула 1.25

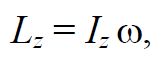
  9. Момент импульса Lz тела относительно оси вращения z:

    Формула 1.26

    где Lz − проекция вектора на ось z; Iz − момент инерции тела относительно оси z; ω – угловая скорость тела.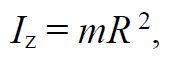
  10. Момент инерции материальной точки относительно оси z:

    Формула 1.27

    где m − масса точки; R − расстояние от точки до оси z.

    Момент инерции твердого тела относительно оси z:

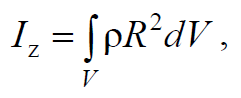
    Формула 1.28

    где ρ – плотность тела; R − расстояние от элемента объема dV тела до оси вращения z.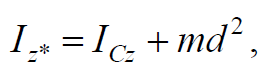
  11. Если ось z* вращения тела не проходит через его центр масс C, то для вычисления момента инерции тела относительно этой оси применяют теорему Штейнера:

    Формула 1.29

    где Iz* − момент инерции относительно заданной оси z*; ICz − момент инерции относительно оси z, параллельной заданной оси z* и проходящей через центр масс тела C; m − масса тела; d − расстояние между осями z и z*.

    Свойство аддитивности момента инерции:

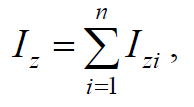
    Формула 1.30

    где Iz – момент инерции системы тел относительно оси z; Izi – момент инерции тела, входящего в систему, относительно данной оси.

    Момент инерции однородного (ρ = const) тела массой m относительно оси z, проходящей через центр масс C тела:

    1. кольцо радиусом R

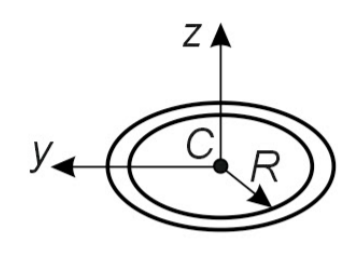
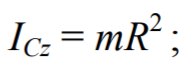
      2. Формула 1.31

    2. диск радиусом R

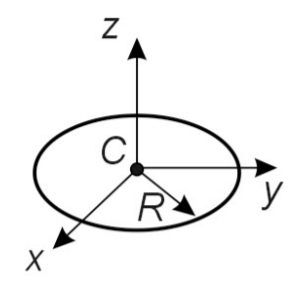
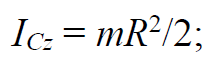
      3. Формула 1.32

    3. стержень длиной l

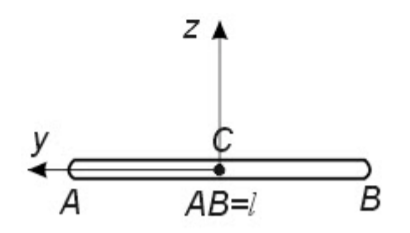
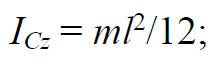
      4. Формула 1.33

    4. шар радиусомR

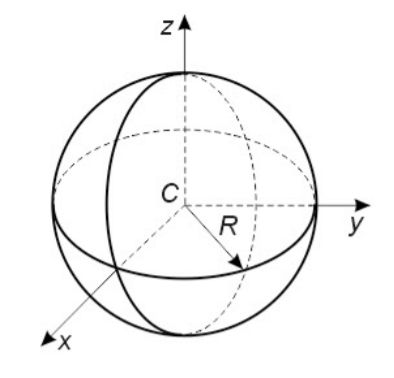
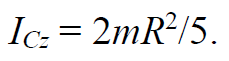
      Формула 1.34

  12. Уравнение движения центра масс тела:

    Формула 1.35

    где F − результирующая всех сил, действующих на тело; aC − ускорение движения центра масс тела.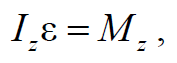
  13. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси вращения z:

    Формула 1.36

    где ε − угловое ускорение тела; Mz − результирующий момент сил, действующих на тело.

Законы сохранения импульса, момента импульса и механической энергии

  1. Механическая система − совокупность материальных точек (тел), взаимодействующих и обменивающихся энергией как между собой, так и с другими телами (внешней средой).

    Силы, которые действуют на материальные точки и тела системы, делятся на внешние и внутренние. Внешними называются силы, которые действуют на точки или тела системы со стороны тел, которые не входят в данную систему. Внутренние силы − это силы взаимодействия между телами и точками рассматриваемой системы. Механическая система называется замкнутой, если внешних сил нет или их векторная сумма равна нулю.

  2. Импульс p и момент импульса L системы тел:

    Формула 1.37

    где pi и Li – импульс и момент импульса i-го тела системы.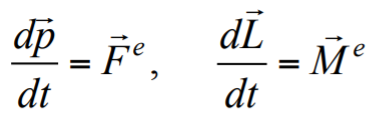
  3. Уравнение изменения импульса и уравнение моментов для системы:

    Формула 1.38

    где Fe и Me – результирующие всех внешних сил и моментов сил, действующих на систему.
  4. Законы сохранения импульса и момента импульса замкнутой механической системы:

    Формула 1.39

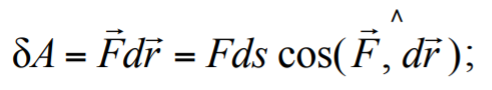
  5. Работа силы F, действующей на материальную точку:
    1. элементарная работа δA силы F на перемещении dr:

      2. Формула 1.40

    2. работа на участке 1-2

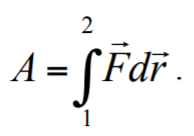
      3. Формула 1.41

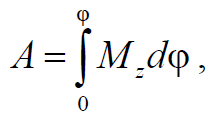
    3. работа сил при повороте твердого тела на конечный угол ϕ относительно неподвижной оси:

      Формула 1.42

      где Mz – момент сил, действующих на тело, относительно данной оси.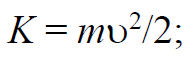
  6. Кинетическая энергия разных материальных объектов:
    1. материальной точки

      2. Формула 1.43

    2. механической системы

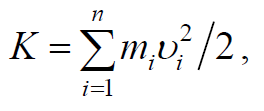
      3. Формула 1.44

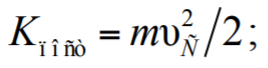
    3. твердого тела при поступательном движении

      4. Формула 1.45

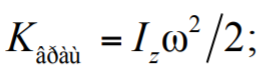
    4. твердого тела при вращательном движении

      5. Формула 1.46

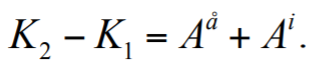
  7. Теорема об изменении кинетической энергии:

    Формула 1.47

    где Ae – работа всех внешних сил; Ai – работа всех внутренних сил.
  8. . Потенциальная энергия П – часть общей механической энергии системы, характеризующая способность тела совершать работу за счет взаимодействия с другими телами.

    Работа консервативных сил равна убыли потенциальной энергии:

    Формула 1.48

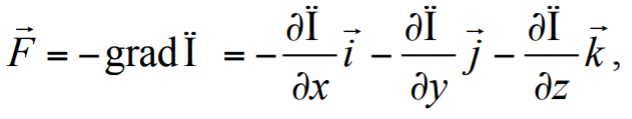
  9. Связь силы с потенциальной энергией:

    Формула 1.49

    где i, j, k – орты декартовой системы координат.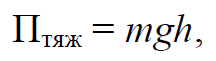
  10. Выражения для потенциальной энергии:
    1. тела массой m в поле силы тяжести Птяж = mgh, (1.50)

      Формула 1.50

      где h – высота тела над уровнем, принятым за нулевой;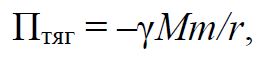
    2. тела массой m в поле силы тяготения

      Формула 1.51

      где γ – гравитационная постоянная; M – масса тела, взаимодействующего сданным телом; r – расстояние между телами;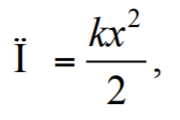
    3. в поле упругой силы

      Формула 1.52

      где k – коэффициент пропорциональности; x – абсолютная деформация.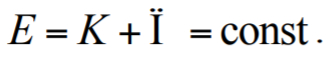
  11. Закон сохранения полной механической энергии E (суммы кинетической и потенциальной энергий) для консервативной системы, на тела которой действуют только консервативные силы (при отсутствии диссипативных сил):

    Формула 1.53

Колебательное движение

  1. Колебательное движение (колебание) − движение материального объекта, обладающее той или иной степенью повторяемости во времени.

    Свободные колебания − колебания, совершающиеся в замкнутой системе за счет первоначально сообщенной энергии и без внешних воздействий.

    Свободные затухающие колебания − колебания, совершающиеся в системе при наличии сил вязкого сопротивления или трения.

    Вынужденные колебания − колебания, возникающие в результате действия внешних (возмущающих) периодически изменяющихся во времени сил.

    Гармонические колебания − колебания, при которых физические величины, их описывающие, изменяются по закону синуса или косинуса.

  2. В случае прямолинейных гармонических колебаний материальной точки ее координата x изменяется по закону:

    Формула 1.54

    где x − отклонение материального объекта от положения равновесия; A − амплитуда, т.е. максимальное отклонение; ω0 = 2πν = 2π/T0 − собственная циклическая частота; T0 − период колебаний; ϕ = (ω0t + α) − фаза колебаний в момент времени t; α − начальная фаза.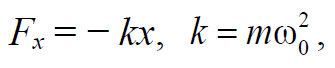
  3. Сила, действующая на частицу, совершающую гармонические колебания, является квазиупругой и называется возвращающей силой:

    Формула 1.55

    где k − коэффициент пропорциональности.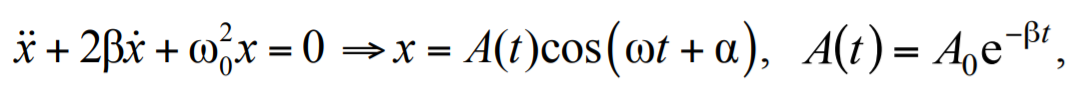
  4. Дифференциальное уравнение прямолинейных затухающих колебаний и его решение:

    Формула 1.56

    где β = µ/2m − коэффициент затухания; µ − коэффициент пропорциональности в формуле для силы сопротивления.

    Период затухающих колебаний:

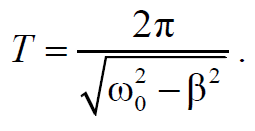
    Формула 1.57

  5. При сложении двух прямолинейных одинаково направленных колебаний x1 = A1 cos(ω0t + α1) и x2 = A2 cos(ω0t + α2) получается результирующее колебание x = A cos(ω0t + α), где

    Формула 1.58

  6. Полная механическая энергия E материальной точки или тела, которые совершают гармонические колебания:

    Формула 1.59

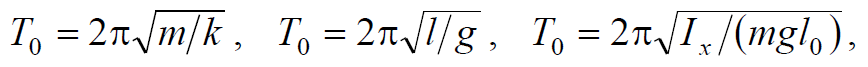
  7. Периоды колебаний пружинного, математического и физического маятников:

    Формула 1.60

    где m − масса колеблющегося тела или материальной точки; k − коэффициент жесткости пружины; l − длина математического маятника; Ix − момент инерции физического маятника относительно горизонтальной оси x подвеса; l0 − расстояние от оси подвеса до центра масс колеблющегося тела.

    Приведенная длина физического маятника:

    Формула 1.61

Гидроаэродинамика

  1. Давление определяется отношением силы Fn, действующей перпендикулярно на некоторую плоскую поверхность с площадью S, к величине этой площади:

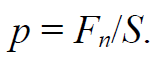
    Формула 1.62

  2. Идеальная жидкость − это жидкость, силы вязкого трения между слоями которой можно не учитывать.

    Идеальная жидкость является несжимаемой, если объем жидкости ∆V не изменяется под действием всестороннего давления ∆p (давления, действующего на некоторую плоскую поверхность с площадью ∆S и не зависящего от ориентации данной плоской поверхности). Плотность ρ идеальной несжимаемой среды является одинаковой во всех точках объема среды и не изменяется в течение всего времени ее движения t: ρ = ρ(x,y,z,t) = const.

    Сжимаемость – свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия k, который выражает относительное изменение объема жидкости V0, отнесенное к единице давления p и определяется по формуле:

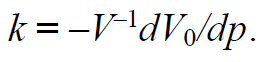
    Формула 1.63

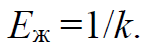
  3. Величина, обратная коэффициенту объемного сжатия, называется объемным модулем упругости жидкости:

    Формула 1.64

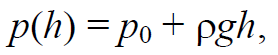
  4. Зависимость давления жидкости от глубины h вычисляется по формуле

    Формула 1.65

    где p0 − внешнее давление; ρgh − гидростатическое давление на глубине h; ρ – плотность жидкости.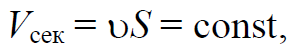
  5. Уравнение непрерывности потока идеальной несжимаемой жидкости:

    Формула 1.66

    где Vсек − объемный секундный расход жидкости; υ − средняя скорость частиц среды; S − площадь поперечного сечения потока.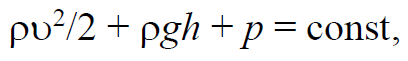
  6. Уравнение Бернулли для идеальной несжимаемой жидкости:

    Формула 1.67

    где ρυ2/2 − динамическое давление.
  7. Если идеальная несжимаемая жидкость, которая находится в широком сосуде с поперечным сечением S1, вытекает из малого отверстия сечением S2, то средняя по сечению отверстия скорость υ жидкости определяется по формуле Торричелли:

    Формула 1.68

    где h − высота столба жидкости.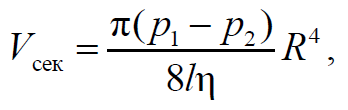
  8. При вязком течении жидкости или газа (при наличии сил вязкого трения) объемный секундный расход Vсек среды через поперечное сечение трубы радиусом R рассчитывается по формуле Пуазейля:

    Формула 1.69

    где p1 - p2 – разность давлений на концах трубы длиной l; η = ρν – коэффициент динамической вязкости среды (ν – коэффициент кинематической вязкости среды).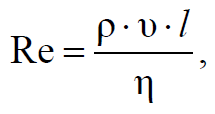
  9. Течение среды называется ламинарным (слоистым), если мысленно выделенные вдоль потока слои не перемешиваются друг с другом (нет вихрей). Если течение среды неустойчиво, то оно становится турбулентным (вихревым), при этом давление в разных точках среды меняется случайным образом, траектории частиц среды представляют собой сложные кривые, слои перемешиваются между собой.

    Режим течения среды зависит от значения величины, называемой числом Рейнольдса:

    Формула 1.70

    где υ – средняя скорость потока среды; l – характерный для поперечного сечения размер.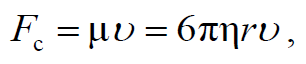
  10. При движении сферического тела в вязкой среде возникает сила сопротивления Fc, модуль которой пропорционален скорости υ и радиусу сферы r (закон Стокса):

    Формула 1.71

    где коэффициент сопротивления µ = 6πηr.

Упругие механические волны

  1. Упругая волна – процесс распространения колебаний частиц сплошной среды.

    Продольная волна – волна, в которой частицы колеблются в направлении распространения волны.

    Поперечная волна – волна, в которой частицы среды колеблются в направлении, перпендикулярном к направлению распространения волны.

    Волновая поверхность – геометрическое место частиц среды, колеблющихся в одинаковой фазе.

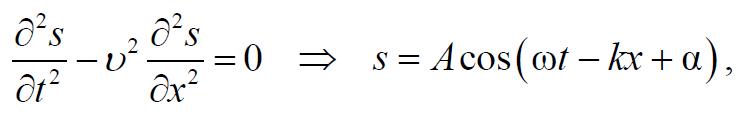
  2. Волновое уравнение и его решение в виде плоской гармонической волны, которая распространяется вдоль оси x с фазовой скоростью υ:

    Формула 1.72

    где s − отклонение частицы от положения равновесия; k = 2π/λ − волновое число.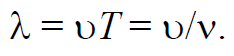
  3. Длиной волны λ, называется расстояние, на которое перемещается волновая поверхность (или фронт волны) за время, равное периоду T колебаний частиц среды:

    Формула 1.73

    где ν = 1/T – частота колебаний.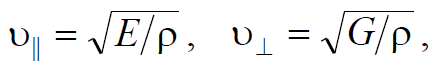
  4. Фазовые скорости распространения волн в однородной среде:
    1. продольных и поперечных волн в твердых телах, соответственно

      Формула 1.74

      где E − модуль Юнга и G − модуль сдвига для твердых тел; ρ − плотность среды.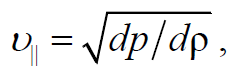
    2. продольных волн в газах

      Формула 1.75

      где p − давление газа; ρ – плотность газа.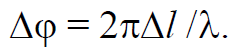
  5. Разность фаз ∆φ колебаний двух точек волны, расстояние между которыми ∆l:

    Формула 1.76

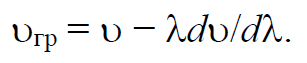
  6. Групповая скорость υгр = dω/dk пакета волн определяется формулой Рэлея:

    Формула 1.77

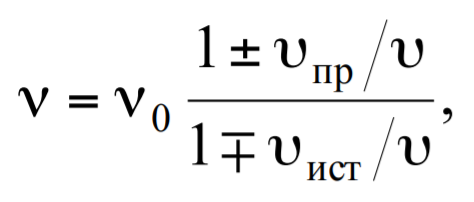
  7. Эффект Доплера − частота ν гармонической волны, воспринимаемая приемником, отличается от частоты ν0 колеблющегося источника волны:

    Формула 1.78

    где υпр и υист − модули скоростей движения приемника и источника соответственно (относительно среды); υ − фазовая скорость монохроматической волны, верхние знаки перед скоростями υпр и υист берутся в том случае, если соответствующая скорость направлена в сторону сближения источника и приемника, в противном случае используется нижний знак.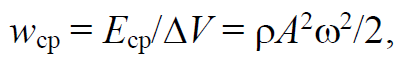
  8. Среднее значение плотности энергии wср упругой волны:

    Формула 1.79

    где Eср − среднее значение полной энергии частиц упругой среды в объеме ΔV; ρ − плотность среды; A – амплитуда волны.

    Волновой поток энергии Фср через перпендикулярную к вектору υ площадку ΔS:

    Формула 1.80

    где Wñð − средняя энергия, переносимая волной через площадку ΔS⊥ за время Δt.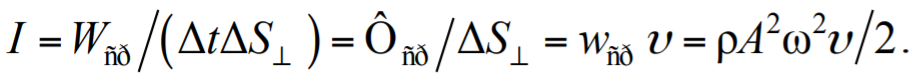
  9. Интенсивность I волны равна средней энергии, которая переносится волной за единицу времени через единичную площадку, расположенную перпендикулярно вектору υ:

    Формула 1.81

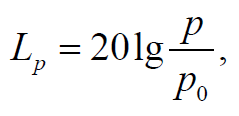
  10. Уровень звукового давления Lp (в децибелах) связан с амплитудой звукового давления p соотношением: ,

    Формула 1.82

    где p − амплитуда звукового давления; p0 – амплитуда звукового давления при нулевом уровне громкости силы звука (пороге слышимости).

    Уровень громкости LI силы звука (в фонах) связан с силой звука I (интенсивностью волны для звукового диапазона) соотношением: ,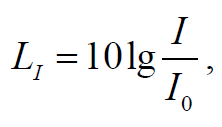

    Формула 1.83

    где I0 – порог слышимости звука (наименьшее значение силы звука, воспринимаемого человеческим ухом).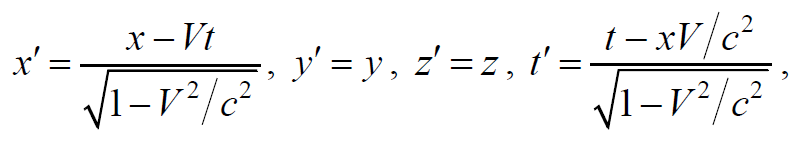

Элементы релятивистской механики

  1. Преобразования Лоренца для координат и времени:

    Формула 1.84

    где $$x^ʹ, y^ʹ, z^ʹ, t^ʹ$$ и $$x, y, z, t$$ – координаты и время одного и того же события в двух инерциальных системах отсчета K и K', двигающихся друг относительно друга со скоростью V; с – скорость света в вакууме.
  2. Лоренцево сокращение длины:

    Формула 1.85

    где l – длина тела в направлении движения; l0 – собственная длина (в системе отсчета в которой тело покоится); υ – скорость тела.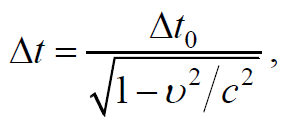
  3. Замедление хода движущихся часов:

    Формула 1.86

    где Δt – длительность процесса в системе отсчета, относительно которой объект движется со скоростью υ; Δt0 – собственное время процесса, измеренное в системе отсчета, в которой объект покоится.
  4. Преобразование скорости в релятивистской механике:

    Формула 1.87

    где $$υ^ʹ_x, υ^ʹ_y, υ^ʹ_z$$ и $$υ_x, υ_y, υ_z$$ – компоненты скорости частицы в двух инерциальных системах отсчета K и K', движущихся друг относительно друга со скоростью V.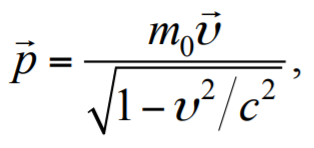
  5. Импульс релятивистской частицы:

    Формула 1.88

    где m0 – масса (покоя) частицы; υ – скорость частицы.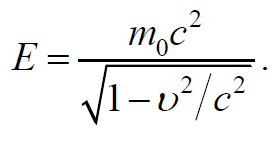
  6. Полная энергия релятивистской частицы:

    Формула 1.89

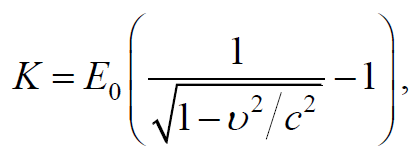
  7. Кинетическая энергия релятивистской частицы:

    Формула 1.90

    где E0 = m0c2 – энергия покоя частицы.
  8. Связь между полной энергией E и импульсом p релятивистской частицы:

    Формула 1.91

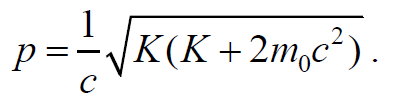
  9. Связь импульса p и кинетической энергии K релятивистской частицы:

    Формула 1.92

Элементы квантовой механики

  1. Длина волны де Бройля для частицы с импульсом p:

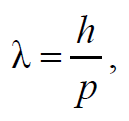
    Формула 1.93

    где h – постоянная Планка.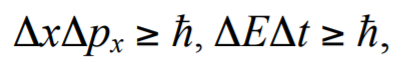
  2. Соотношения неопределенностей Гейзенберга:

    Формула 1.94

    где Δx и Δpx – неопределенности координаты и соответствующей компоненты импульса; ΔЕ – неопределенность измерения энергии за промежуток времени Δt; ħ = h/2π – постоянная Планка.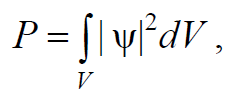
  3. Вероятность обнаружить частицу в объеме V:

    Формула 1.95

    где |ψ|2 = ψψ* – плотность вероятности обнаружить частицу в некоторой точке пространства; ψ(x, y, z, t) – волновая функция частицы; ψ* – комплексно сопряженная ей функция.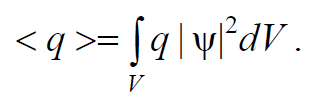
  4. Среднее значение величины q, являющейся функцией координат:

    Формула 1.96

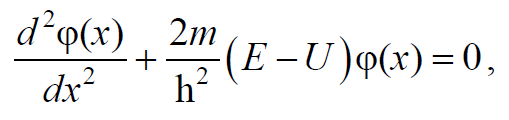
  5. Одномерное уравнение Шредингера для стационарных состояний:

    Формула 1.97

    где ϕ(x) – волновая функция, описывающая стационарное состояние частицы; m – масса частицы; E – полная энергия частицы; U = U(x) – потенциальная энергия частицы.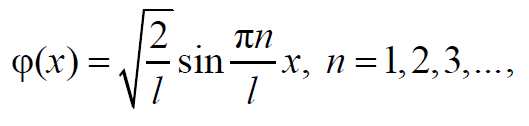
  6. Волновая функция ϕ(x), описывающая стационарные состояния частицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками:

    Формула 1.98

    где n – главное квантовое число; l – ширина ямы.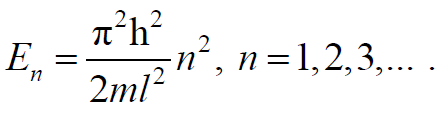
  7. Энергия En частицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками:

    Формула 1.99

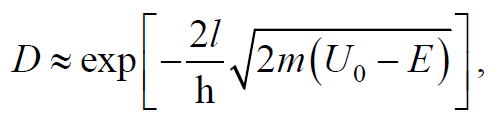
  8. Коэффициент прозрачности D прямоугольного потенциального барьера высотой U0 и шириной l:

    Формула 1.100

    где m – масса частицы, E – энергия частицы.