



Пусть в некоторой среде распространяется в направлении оси 0х плоская продольная волна S=Acos(ωt−kx+φ). Выделим в среде элементарный объем ΔV, настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными. Выделенный объем обладает кинетической энергией K=12mv2. Если масса m=ρΔV, а v=∂S∂t, то
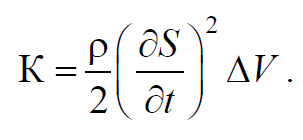
Формула 6.5.1
Потенциальная энергия упругой деформации рассматриваемого объема
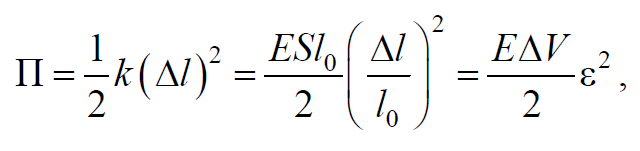
Формула 6.5.2
где k=ESl0; l0 − первоначальная длина рассматриваемого объема; ε=Δll0 − относительная деформация объема; ΔV=Sl0 − первоначальный объем. Используя формулу 6.4.8 и, учитывая, что ε=∂S∂x, получим
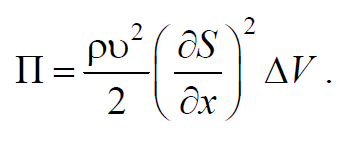
Формула 6.5.3
Тогда полная энергия упругой волны
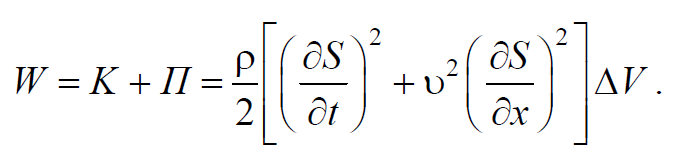
Определим плотность энергии, разделив 6.5.4 на объем ΔV
Формула 6.5.4
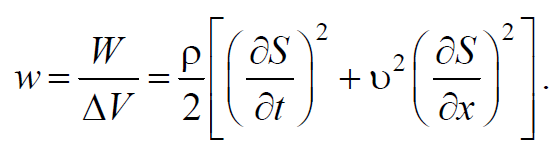
Формула 6.5.5
Продифференцируем уравнение плоской продольной волны 6.2.8 по времени t и по координате х и подставим выражения в формулу 6.5.5 учтя, что k2υ2=ω2
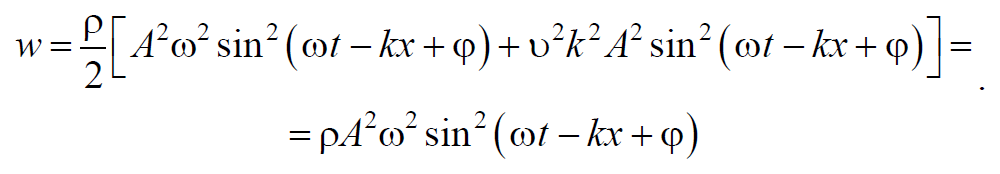
Формула 6.5.6
Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно
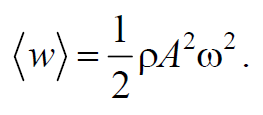
Формула 6.5.7
Таким образом, плотность энергии и среднее значение плотности энергии пропорциональны плотности среды ρ, квадрату частоты ω и квадрату амплитуды волны А.
Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Поток энергии Ф через данную поверхность равен энергии dW переносимой за время dt
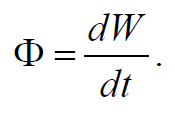
Формула 6.5.8
Ф измеряется в ваттах.
Для характеристики распространения энергии в разных точках пространства вводится векторная величина, называема плотностью потока энергии. Плотность потока энергии численно равна потоку энергии через единичную площадку ΔS, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.
Если через площадку ΔS, перпендикулярную к направлению распространения волны, переносится энергия ΔW за время Δt, то плотность потока энергии равна
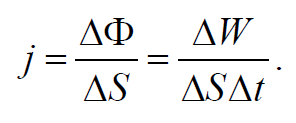
Формула 6.5.9
Рассмотрим объем цилиндра с основанием ΔS и высотой υΔt (υ − фазовая скорость волны). В случае малого объема цилиндра, плотность энергии во всех точках цилиндра можно было считать одинаковой и поэтому энергию можно найти как произведение плотности энергии ω на объем ΔV=ΔSυΔt
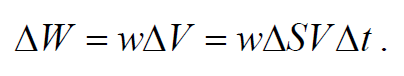
Формула 6.5.10
Подставив выражение 6.5.10 в последнее выражение, получим
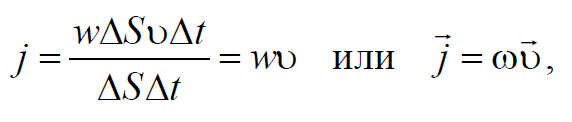
Формула 6.5.11
где j − вектор плотности потока энергии, называемый вектором Умова.
Интенсивность волны равна
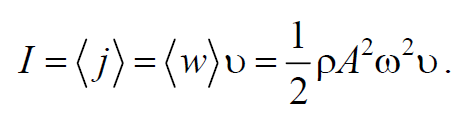
Формула 6.5.12
Данное выражение справедливо для волны любого вида.
Определим поток энергии через поверхность S. Для этого разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW. Объем цилиндра, где вычисляется энергия, равен dV=υdtdScosϕ. Тогда в этом объеме содержится энергия
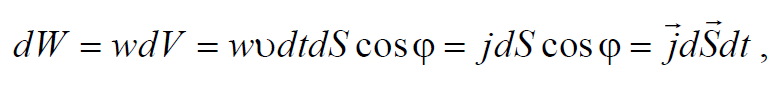
Формула 6.5.13
где d S=ndS; n − единичный вектор нормали к поверхности dS.
Поток энергии через элементарную поверхность dS
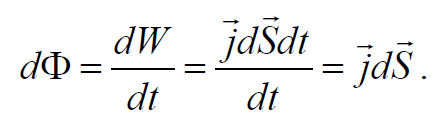
Формула 6.5.14
Поток энергии через поверхность S равен
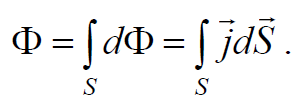
Формула 6.5.15
Скорость распространения волны есть скорость перемещения фазы и называется фазовой скоростью. Фазовая скорость равна
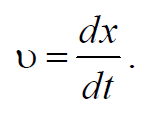
Формула 6.6.1
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, и к ним применим принцип суперпозиции волн: при распространении в линейной среде т.е.средеснеизменяющимисясвойствами нескольких волн, каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Используя принципа суперпозиции, любая волна может быть представлена в виде волнового пакета. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Простейший волновой пакет двух распространяющихся вдоль положительного направления оси Х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем
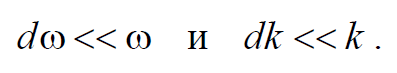
Формула 6.6.2
Тогда
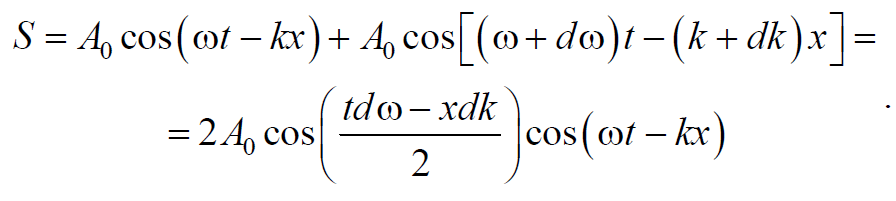
Формула 6.6.3
Эта волна отличается от гармонической тем, что ее амплитуда
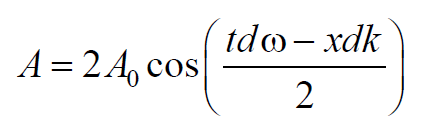
Формула 6.6.4
медленно изменяющаяся функция координаты х и времени t.
За скорость распространения волнового пакета принимают скорость перемещения максимума амплитуды волны. При условии, что tdω−xdk=const, получим
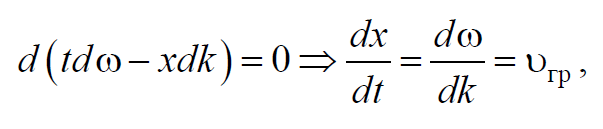
Формула 6.6.5
где υгр – групповая скорость. Рассмотрим связь между групповой и фазовой скоростями. Учитывая, что волновое число k=2πλ и dk=−2πλ2dλ=−kλdλ, получим
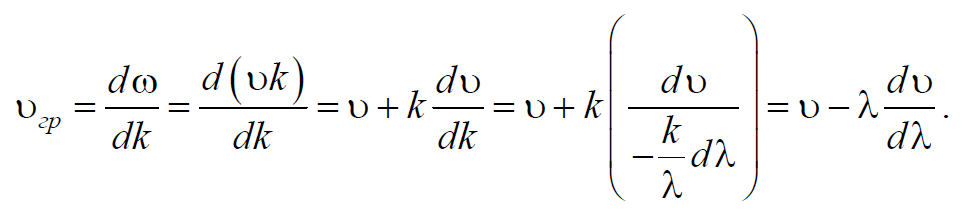
Формула 6.6.6
В теории относительности доказывается, что групповая скорость υгр ≤ c, в то время как для фазовой скорости ограничений не существует.
Для того чтобы рассмотреть интерференцию волн, введем понятие когерентности. Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связано с понятием когерентности. Волны называются когерентными, если разность их фаз остается постоянной во времени. При наложении в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн, и заключается в том, что колебания в одних точках усиливают, а в других ослабляют друг друга.
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S1 и S2, колеблющимися с одинаковыми амплитудой, частотой, нулевой начальной фазой и постоянной разностью фаз. Запишем уравнения колебаний:
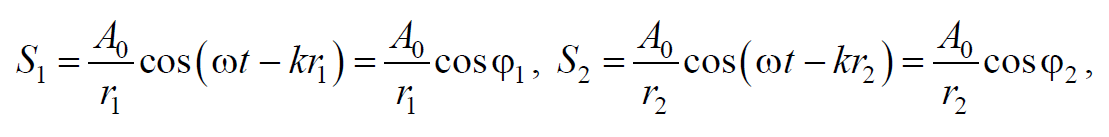
Формула 6.7.1
где r1 и r2 − расстояния от источников волн до рассматриваемой точки.
Амплитуда результирующей волны равна сложениеодинаковонаправленныхколебаний
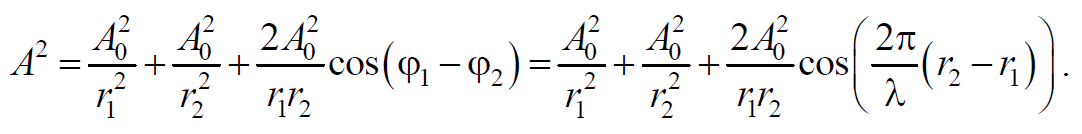
Формула 6.7.2
Так как разность начальных фаз (ϕ1−ϕ2)=2πλ(r2−r1)=2πλΔ=const, то результат наложения двух волн в различных точках зависит от величины Δ=r2−r1, называемой разностью хода волн.
В точках, где выполняется условие
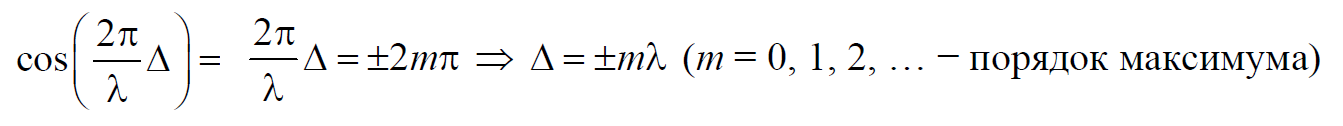
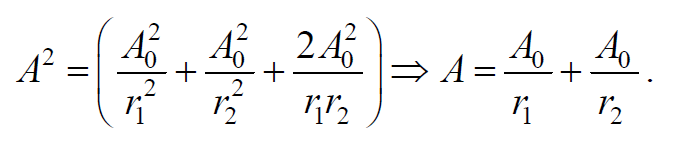
Формула 6.7.3
Так как квадрат амплитуды колебаний пропорционален интенсивности волны, то получаем
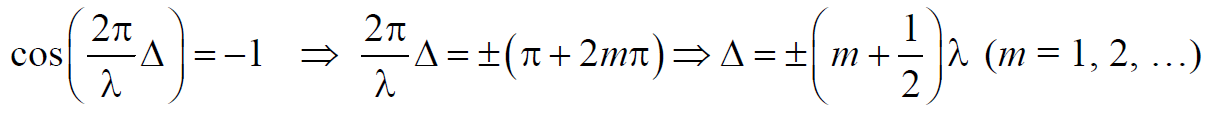
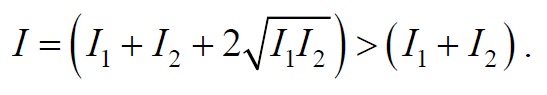
Формула 6.7.4
То есть наблюдается усиление интенсивности увеличениеамплитуду результирующей волны или интерференционный максимум.
2) В точках, где выполняется условие
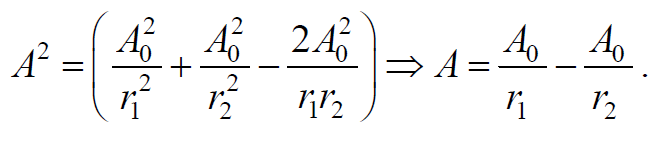
Формула 6.7.5
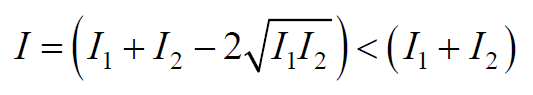
Формула 6.7.6
То есть наблюдается ослабление интенсивности уменьшениеамплитуды результирующей волны или интерференционный минимум.
Таким образом, в результате наложения двух когерентных волн в среде возникают колебания, амплитуда которых различна в разных точках среды, при этом в каждой точке среды получается или максимум амплитуды, или минимум амплитуды, или ее промежуточное значение − в зависимости от значения разности расстояний точки до когерентных источников. Интерференция света приводит к перераспределению энергии волны между соседними областями, хотя в среднем для больших областей энергия остается неизменной.
Рассмотрим интерференцию стоячих волн. Стоячие волны − это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Запишем уравнение двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях
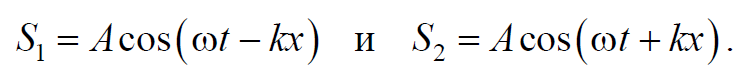
Формула 6.8.1
Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны
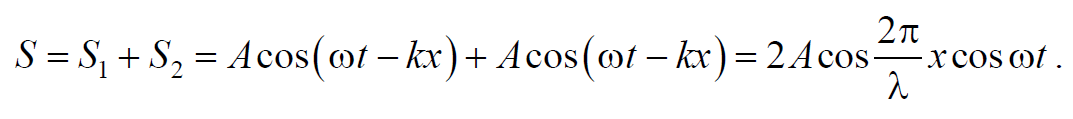
Формула 6.8.2
Из данного уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда зависит от координаты х
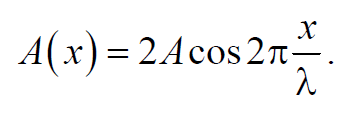
Формула 6.8.3
Точки, в которых амплитуда колебаний достигает максимального значения и координаты которых удовлетворяют условию
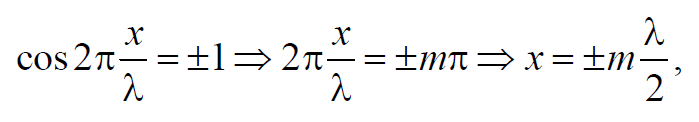
Формула 6.8.4
где m = 0, 1, 2, … называются пучностями стоячей волны.
Точки, в которых амплитуда колебаний обращается в нуль и координаты которых удовлетворяют условию
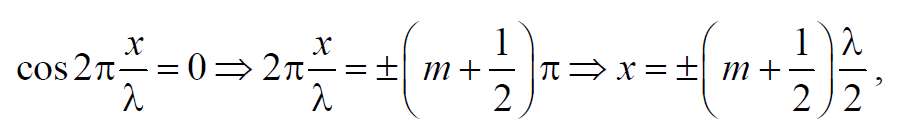
Формула 6.8.5
где m = 0, 1, 2, … называются узлами стоячей волны.