



Принцип относительности СТО предполагает, что все уравнения релятивистской динамики должны быть инвариантными относительно преобразований Лоренца. Поэтому инвариантность формулируемых законов движения в релятивистской механике является определяющим критерием того, что они правильно отражают физическую реальность.
В классической механике Ньютона импульс определяется соотношением $$\vec{p}=m\vec{υ}$$. Требование, что в релятивистской механике (как и в механике Ньютона) для изолированной системы тел в любой инерциальной системе отсчета выполнялся закон сохранения импульса, и учет законов преобразования скоростей при переходе из одной системы отсчета в другую, приводит к тому, что импульс релятивистской частицы будет определяться выражением
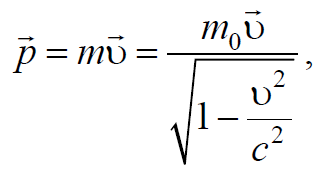
Формула 7.6.1
где $$m={m_0 \over \sqrt{1-{υ^2 \over c^2}}}$$ − релятивистская масса движущейся частицы; m0 − массой покоя частицы, т. е. масса частицы в собственной системе отсчета.
Выражение (7.6.1) позволяет сделать важнейший вывод: в релятивистской динамике масса частицы зависит от скорости ее движения. При υ << c (это соотношение всегда выполняется в классической механике), получаем m = m0 = const.
Первый закон Ньютона, являющийся выражением принципа относительности, сохраняет свою классическую формулировку в релятивистской динамике.
Выражение для второго закона Ньютона в релятивистской механике также сохраняет свою классическую формулировку при условии, что импульс определяется по формуле (7.6.1)
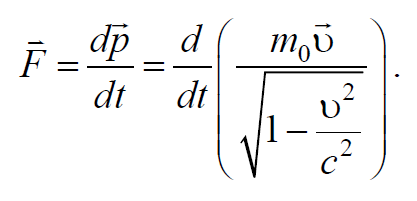
Формула 7.7.1
Релятивистское уравнение (7.7.1) инвариантно относительно преобразований Лоренца.
Третий закон Ньютона в релятивистской динамике справедлив только для контактных сил. В классической механике для сил, действующих на расстоянии, предполагается мгновенная передача взаимодействия без материального посредника. Это несовместимо с релятивистским положением о том, что максимальная скорость передачи взаимодействия не может быть больше скорости света в вакууме. Поэтому для взаимодействий с конечной скоростью распространения третий закон Ньютона в своей классической формулировке неприменим.
Понятие энергии в релятивистской механике сохраняет тот же смысл, что и в классической механике. Однако требование инвариантности уравнений релятивистской механики относительно преобразований Лоренца приводит к установлению взаимосвязи между энергией E и массой m частицы, а также к изменению выражения для ее кинетической энергии К.
Найдем выражение для кинетической энергии материальной точки в релятивистской механике. Изменение кинетической энергии материальной точки при элементарном перемещении $$d\vec{r}$$ равно работе, совершаемой силой $$\vec{F}$$, действующей на точку, при этом перемещении
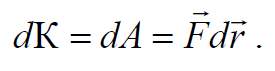
Формула 7.8.1
Воспользуемся релятивистским выражением второго закона Ньютона (7.7.1), и с учетом $$d\vec{r}=\vec{υ}dt$$ получаем

Формула 7.8.2
С учетом $$\vec{υ}d\vec{υ}=d({υ^2 \over 2})$$ из выражения (7.8.2) получаем

Формула 7.8.3
Интегрирование уравнения (7.8.3) приводит к выражению
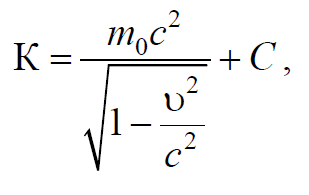
Формула 7.8.4
где С – постоянная интегрирования.
Найдем постоянную интегрирования С. Для этого воспользуемся условием, что при υ = 0 кинетическая энергия К должна быть тоже равна нулю. С учетом этого из выражения (7.8.4) получаем $$C=-m_0c^2$$. Таким образом, релятивистское выражение для кинетической энергии имеет вид
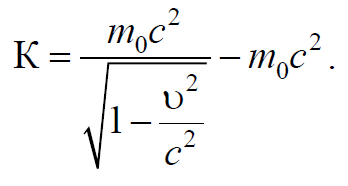
Формула 7.8.5
Величина
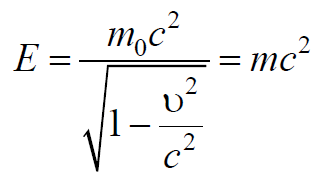
Формула 7.8.6
называется полной энергией свободной частицы (при отсутствии внешних полей).
Величина
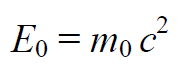
Формула 7.8.7
называется энергией покоя (при υ = 0).
С учетом формул (7.8.6, 7.8.7) выражение для кинетической энергии (7.8.5) можно записать в виде
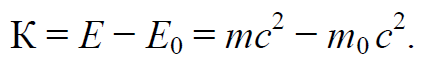
Формула 7.8.8
При υ << c, с учетом получаем $$(1-{υ^2 \over c^2})^{1 \over 2}=1+{1 \over 2}{υ^2 \over c^2}+...,$$ выражение для кинетической энергии в классической механике
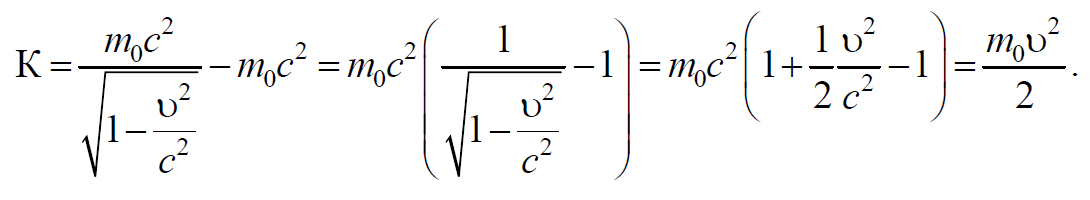
Формула 7.8.9
Таким образом, при малых скоростях движения материальной точки ее кинетическая энергия, вычисленная по релятивистской формуле (7.8.5), совпадает с выражением (7.8.9) для энергии в классической механике.
Из соотношения (7.8.6) следует также важный вывод: энергия тела пропорциональна его релятивистской массе. Всякое изменение энергии тела сопровождается изменением его релятивистской массы и, наоборот, всякое изменение релятивистской массы сопровождается изменением энергии тела
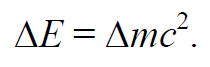
Формула 7.8.10
Это утверждение носит название закона взаимосвязи релятивистской массы и энергии.
Для установления взаимосвязи между энергией и импульсом частицы возведем в квадрат выражение для релятивистской массы $$m={m_0 \over \sqrt{1-{υ^2 \over c^2}}}$$. Тогда получим
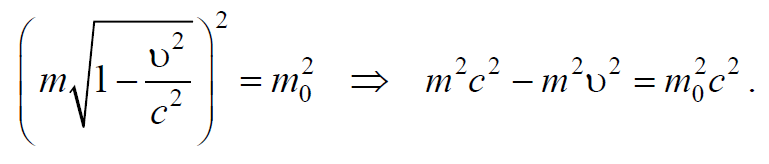
Формула 7.9.1
Умножим выражение (7.9.1) на c2 и преобразуем
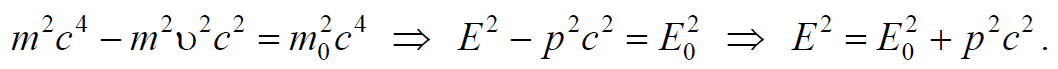
Формула 7.9.2
Используя выражение (7.9.2) можно выразить энергию частицы через ее импульс
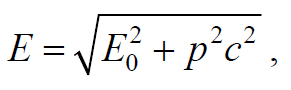
Формула 7.9.3
или импульс частицы через ее энергию
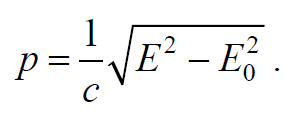
Формула 7.9.4
А с учетом выражения (7.8.8) из (7.9.4) получим
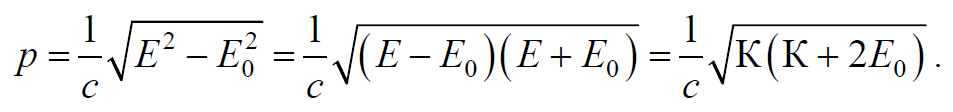
Формула 7.9.5