Рассмотрим волновую функцию свободной микрочастицы, которая имеет определенные значения импульса р и энергии Е, т. е. движется со скоростью υ, например, вдоль оси Ох (ру = рz = 0). Так как из опытов следует, что параллельный пучок элементарных частиц обладает свойствами плоской волны распространяющейся в направлении скорости частиц, то рассмотрим в общем виде плоскую волну распространяющуюся вдоль Ох. Запишем волновую функцию свободной частицы в комплексном виде по аналогии с уравнением плоской волны
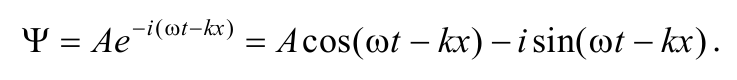
Формула 8.6.1
Преобразуем выражение (8.6.1), используя формулы взаимосвязи импульса р и энергии Е частицы (корпускулярных характеристик) с волновым числом k и циклической частотой ω (с волновыми характеристиками частицы)
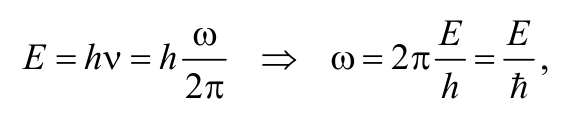
Формула 8.6.2
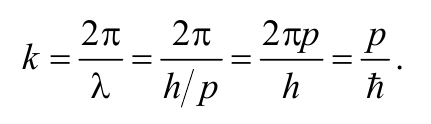
Формула 8.6.3
Подставим (8.6.2−8.6.3) в уравнение (8.6.1) и получим
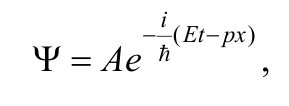
Формула 8.6.4
где $${ħ} = {h \over 2π}$$ − постоянная Планка.
Представим уравнение (8.6.4) в виде
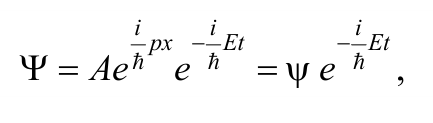
Формула 8.6.5
где $${Ψ} = Ae^{{i \over ħ}px}$$ − амплитудная часть волновой функции, зависящая только от координаты.
Применим к ψ оператор Лапласа
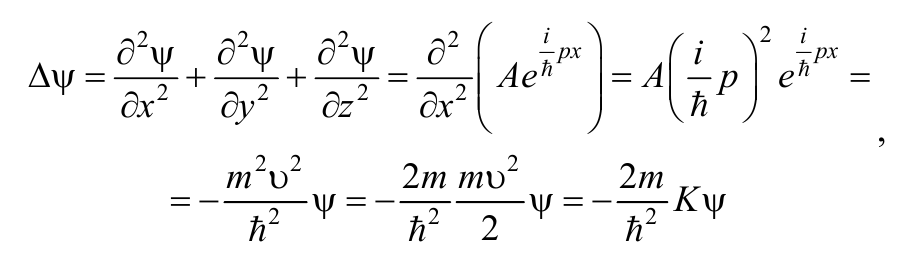
Формула 8.6.6
и получим уравнение Шредингера для свободной частицы
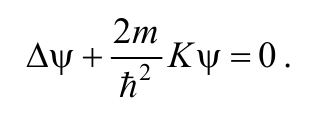
Формула 8.6.7
Обобщим это уравнение для несвободной частицы, заменив кинетическую энергию К на разность между полной энергией Е и потенциальной энергией U
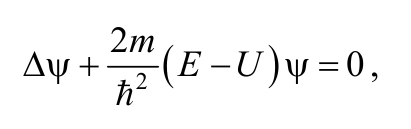
Формула 8.6.8
где U − потенциальная энергия частицы в стационарных потенциальных силовых полях
Уравнение (8.6.8) является стационарным уравнением Шредингера. Изложенные выше рассуждения не могут рассматриваться как вывод уравнения Шредингера. Однако они показывают, на примере свободной частицы, каким образом можно прийти к установлению этого уравнения.
Открытие корпускулярно-волнового дуализма стало важным шагом для понимания того, что присущее классической физике противопоставление частиц и волн не имеет места для объектов микро-мира. Электроны, фотоны, нейтроны и другие микрочастицы в одних случаях ведут себя как частицы, в других проявляют свои волновые свойства. Это значит, что объекты микромира не являются ни класси-ческими частицами, ни классическими волнами и для изучения их свойств не применимы ни классические методы описания частиц, ни классические методы описания волн. В этом случае состояние микро-частиц описывается волновой функцией Ψ (волнами материи).
Рассмотрим состояния свободной микрочастицы, описываемой волной де Бройля (8.6.1), запишем волновую функция для частицы и комплексно сопряженную ее волновую функцию
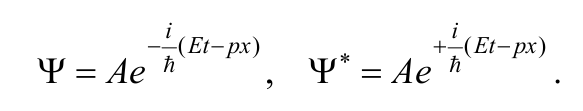
Формула 8.7.1
Найдем плотность вероятности обнаружения микрочастицы на оси Ох:
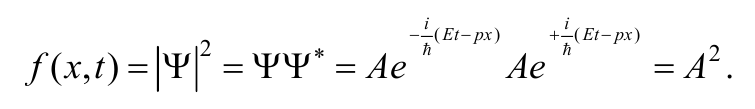
Формула 8.7.2
Таким образом, свободная микрочастица с импульсом р и энергией Е с одинаковой плотностью вероятности может быть обнаружена в любой точке оси Ох.
Из выражения (8.7.2) следует, если вектор импульса p постоянен (свободная частица), то ее квантово-механическое состояние описывается плоской волной де Бройля (8.6.1), которая приводит к однородному распределению плотности вероятности. Поскольку плотность вероятности обнаружить такую квантовую частицу в каждой точке бесконечного пространства одинакова, мы фактически ничего не можем сказать о ее координате х в любой заданный момент времени t, т. е. при фиксированном значении импульса координатах частицы не определена. Это один из примеров «парадоксов квантовой механики» (в классической механике Ньютона каждому значению координаты х соответствует определенное значение импульса движущейся частицы).
Таким образом, частица не имеет определенных значений координаты, импульса, энергии. Можно лишь в общем случае утверждать, что значения x, y, z, p, E лежат в пределах соответствующих интервалах координат (Δх, Δу, Δz), импульса (Δрх, Δрy, Δрz) и энергии (ΔЕ), которые связаны соотношениями неопределенностей Гейзенберга:
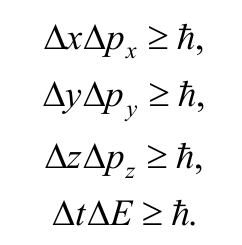
Формула 8.7.3
В соответствии с формулами (8.7.3) принцип Гейзенберга гласит: любая квантовая система не может находиться в состояниях, в которых координаты ее центра инерции (для частицы − координаты частицы) и импульс одновременно принимают вполне определенные значения.
Это значит, что для квантовой частицы нельзя одновременно указать точные значения координат и проекций импульса. В квантовой механике теряет смысл понятие траектории движения частицы, так как если мы точно определим значения координат, то ничего не сможем сказать о направлении ее движения (т. е. импульсе), и наоборот.
Уравнения (8.4.1) и (8.4.6) являются сложными дифференциальными уравнениями в частных производных. Известны аналитические решения только для очень простых зависимостей потенциальной энергии.
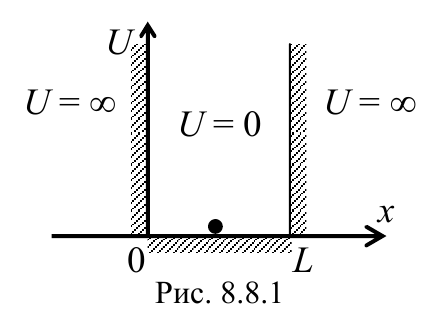
Рассмотрим следующую задачу: частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками (рис. 8.8.1). Потенциальной ямой с бесконечно высокими стенками называется область пространства, в которой потенциальная энергия определена соотношениями
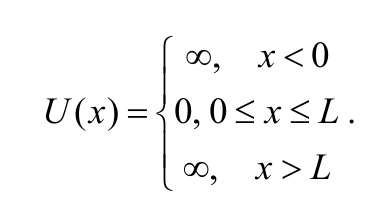
Формула 8.8.1
В одномерном случае U = U(x), ψ = ψ(x), $${ΔΨ} = {{{d^2}{Ψ}} \over dx^2}$$, поэтому стационарное уравнение Шредингера (8.4.6) примет вид
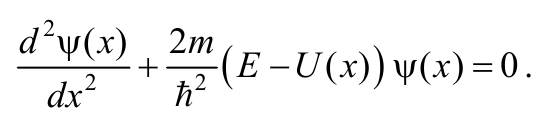
Формула 8.8.2
Поскольку потенциальная энергия U за границами ямы бесконечно велика, то вероятность нахождения частицы за пределами ямы равна нулю. Тогда значения функции ψ на границах ямы (в точках с координатами х = 0 = L) должны быть равны нулю, т. е. получаем граничные условия для собственной волновой функции ψ(х):
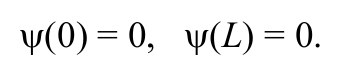
Формула 8.8.3
Так как внутри ямы U = 0, то уравнение (8.8.2) примет вид
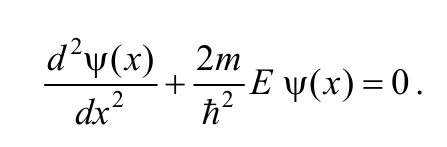
Формула 8.8.4
Обозначим
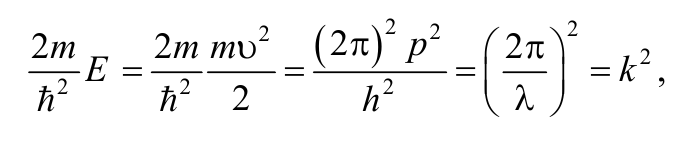
Формула 8.8.5
с учетом этого получает дифференциальное уравнение вида
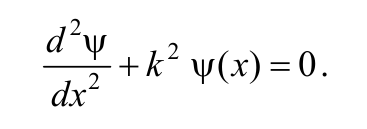
Формула 8.8.6
Общее решение дифференциального уравнения (8.8.6) имеет вид
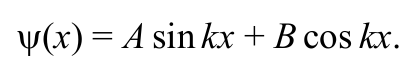
Формула 8.8.7
Подставим в формулу (8.8.7) первое граничное условие из (8.8.3)
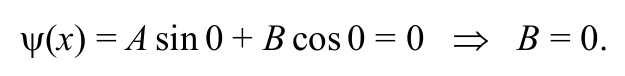
Формула 8.8.8
С учетом второго граничного условия из (8.8.3) решение уравнения (8.8.8) будет иметь вид
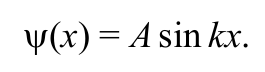
Формула 8.8.9
Подставим второе граничное условие (8.8.3) в выражение (8.8.9)
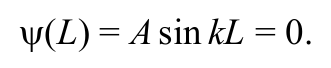
Формула 8.8.10
Выполнения условия (8.8.10), возможно лишь в случае, если
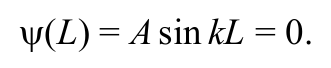
Формула 8.8.11
Значение n = 0 отпадает, поскольку при этом получается ψ = 0 − частица нигде не находится.
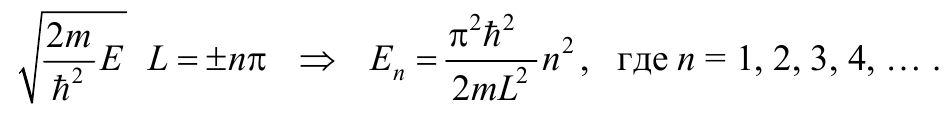
Формула 8.8.12
Из выражения (8.8.12) видно, что спектр собственных энергий частицы в рассматриваемой потенциальной яме является дискретным. Этот результат согласуется с гипотезой Планка о квантовании энергии и является характерным свойством уравнения Шредингера. Также следует отметить то факт, что энергия микрочастицы в состоянии с наименьшим значением n = 1 (в основном состоянии) не равна нулю.
Число n, определяющее допустимые значения энергий микро-частицы, называется главным квантовым числом. Квантовое стационарное состояние с заданным значением n имеет фиксированное значение энергии Еn (Еn = const). Состояние с фиксированной энергией соответствует в классическом случае движению частицы некоторой орбите, параметры которой удовлетворяют закону сохранения энергии (К + П = const).
Из выражения (8.8.11) следует, что волновое число
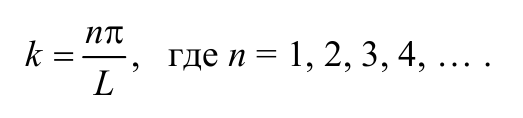
Формула 8.8.13
Так как волновое число k связано с длиной волны де Бройля λБр соотношением
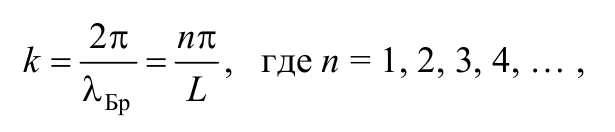
Формула 8.8.14
то соответствующие длины волн де Бройля должны удовлетворять условию, при котором
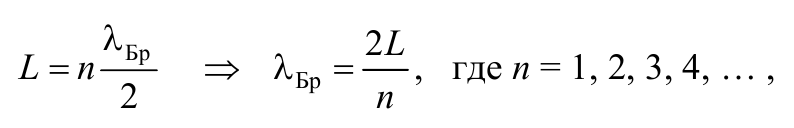
Формула 8.8.15
т. е. на ширине L потенциальной ямы должно укладываться целое число полуволн де Бройля, (или целое число стоячих волн де Бройля).
Найдем выражение для волновой функции частицы, находящейся в бесконечной потенциальной яме. Подставим выражение (8.8.14) в выражение (8.8.9)
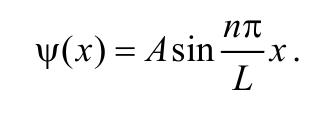
Формула 8.8.16
Найдем Для нахождения значения А воспользуемся условием нормировки волновой функции (8.3.7)
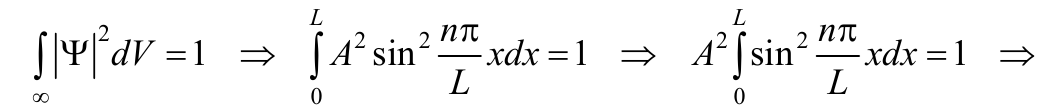
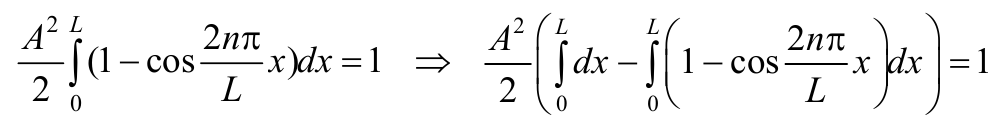
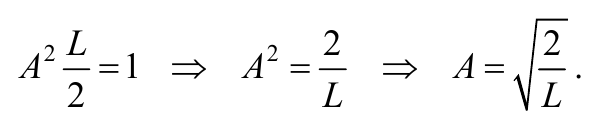
Формула 8.8.17
Подставим (8.8.17) в выражение (8.8.16) и получим
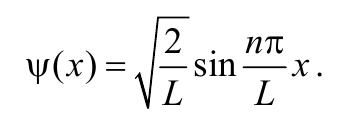
Формула 8.8.18
Полное выражение для волновой функции будет иметь вид
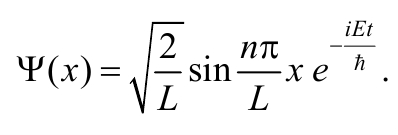
Формула 8.8.19
Квадрат модуля волновой функции, который является плотностью вероятности нахождения частицы заданной точке пространства, равен
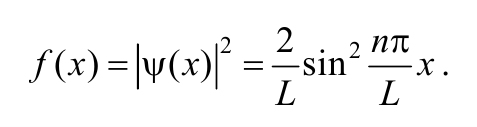
Формула 8.8.20
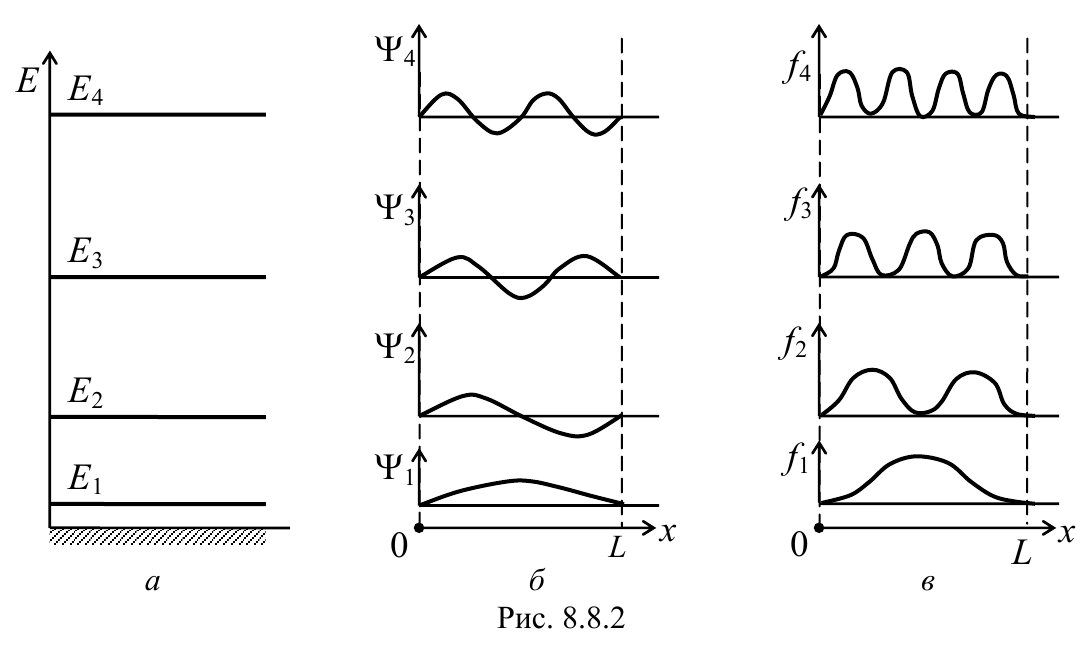
Построим для четырех первых квантовых состояний (n = 1, 2, 3, 4) уровни спектра энергий (рис. 8.8.2, а), волновые функции (рис. 8.8.2, б) и плотность вероятности нахождения частицы заданной точке (рис. 8.8.2, в).