



Измерением называют процесс получения значения физической величины опытным путем. По существу, измерение представляет собой последовательность экспериментальных и вычислительных операций, проводимых с целью нахождения значения физической величины.
По способу получения значения измеряемой величины различают прямые и косвенные измерения. Прямыми называют измерения, в результате которых значение измеряемой величины определяется непосредственно из опыта, с помощью прибора, шкала которого проградуирована в единицах измеряемой величины (измерение длины – штангенциркулем, температуры – термометром и т. д.). Косвенные − это такие измерения, в которых физическая величина вычисляется по формуле, содержащей физические величины, определяемые путем прямых измерений (например, нахождение скорости υ движения по пройденному расстоянию l и времени t движения, сопротивления резистора R по измерению силы тока I и напряжения U и т. д.).
Физическую величину нельзя измерить абсолютно точно. Всегда имеется некоторая погрешность (ошибка) измерения, обусловленная ограниченной точностью измерительных приборов, а также несовершенством используемой методики измерения. Поэтому в задачу измерений входит не только нахождение значения физической величины, но и оценка допущенной при измерении погрешности.
Абсолютной погрешностью измерения называют разность между результатом измерения физической величины х и ее истинным значением хист:
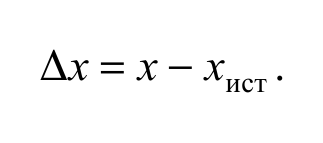
Формула O1
Причем истинное значение, а следовательно, и абсолютная погрешность принципиально неизвестны и подлежат оценке по результатам измерений.
Точность измерений величины х характеризуют относительной погрешностью
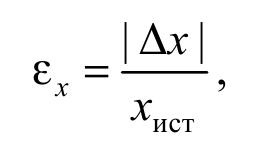
Формула O2
которая показывает, какую часть абсолютная погрешность составляет от истинного значения.
По характеру проявления погрешности физических измерений принято подразделять на систематические, случайные и промахи.
Систематические погрешности − это такие погрешности, у которых значения и знак остаются постоянными на протяжении одной серии измерений. Они вызываются постоянно действующими причинами, односторонне влияющими на результат измерений, и зависят от точности приборов и качества используемых методик измерений. Примеры причин возникновения систематической погрешности: неточная установка прибора на ноль перед измерением, секундомер отстает или спешит, не учитываются силы трения и сопротивления в методе измерения, сопротивления соединительных проводов и контактов и т. д. Систематические погрешности можно выявить, проводя измерения различными методами и приборами с последующим анализом результатов измерений.
Случайные погрешности − это погрешности, которые изменяются от опыта к опыту непредсказуемым (случайным) образом. Причем с равной вероятностью они могут быть как положительными, так и отрицательными. Случайная погрешность возникает как результат совместного влияния различных случайных, меняющихся от измерения к измерению, и не контролируемых экспериментатором факторов, оказывающих действие на процесс измерения. Одна из причин случайной погрешности – непостоянство физических условий, в которых производятся измерения. Например, небольшие колебания температуры воздуха и его давления, электрического напряжения в сети, механические колебания и т. п. Случайную погрешность значения измеряемой величины можно уменьшить многократным повторением измерения.
Промахи (грубые ошибки) − это большие по значению погрешности, сильно искажающие результат. Как правило, промахи вызываются невнимательностью экспериментатора (неправильный отсчет по шкале прибора или небрежная запись в таблице). Они могут возникать также вследствие неисправности приборов. Результаты измерений, содержащие промахи, отбрасываются, как не внушающие доверия.
В случае прямых многократных измерений физической величины x получают набор из n ее значений: x1, x2, …, xn. Наилучшей оценкой истинного значения измеряемой величины по выполненной серии измерений является среднее арифметическое x этих значений:
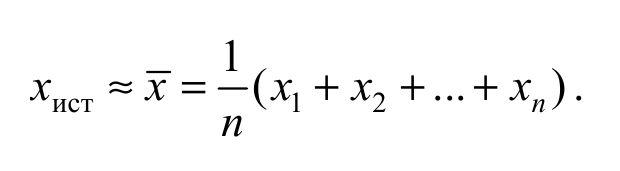
Формула O3
Погрешность среднего арифметического значения обусловлена случайными и систематическими составляющими.
Случайная погрешность Δxсл среднего арифметического значения x вычисляется по формуле
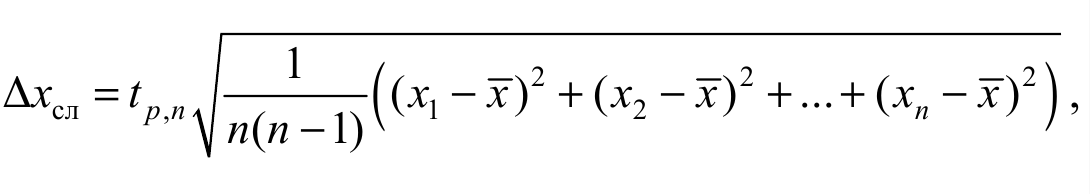
Формула O4
где tp, n – коэффициент Стьюдента, зависящий от числа измерений n и заданной доверительной вероятности р, с которой истинное значение физической величины x лежит в интервале x −Δxсл ≤ x ≤ x + Δxсл.
Значения коэффициента Стьюдента при различных р и n приведены в таблице. Величина доверительной вероятности р выбирается экспериментатором самостоятельно и может принимать любые значения от нуля до единицы.
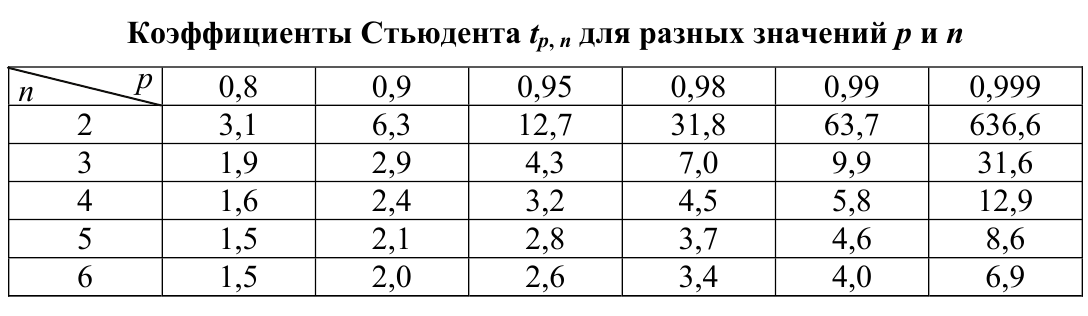
Чем больше р, тем более сильное утверждение делается о измеряемом значении x, к чему и надо стремиться. Обычно при выполнении учебных лабораторных работ выбирают р = 0,95.
Систематическая погрешность метода измерений может быть учтена в результате тщательного анализа модельных представлений, положенных в основу процесса измерений. Совершенствование метода измерений и введение уточнений в расчетную формулу позволяет уменьшить систематическую погрешность.
Систематическая погрешность приборов и измерительных инструментов (приборная или инструментальная погрешность) вызвана неточностью градуировки шкалы, качества изготовления, сборки и подгонки отдельных деталей приборов и других причин технологического характера. При определении приборных погрешностей Δxпр необходимо учитывать следующее:
a) для высокоточных (прецизионных) приборов в техническом паспорте на прибор приводятся погрешности для всех диапазонов измеряемой величины;
б) для механических измерительных приборов (линейка, штангенциркуль, микрометр, секундомер и т. д.), не имеющих паспорта, можно считать, что абсолютная приборная погрешность
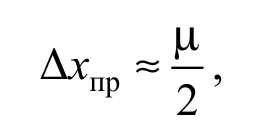
Формула O5
в) для стрелочных электроизмерительных приборов абсолютная приборная погрешность определяется по их классу точности Епр, который указан на шкале прибора (обычно в правом нижнем углу, цифры могут быть помещены в кружок или ромбик). Класс точности Епр показывает, какой процент от наибольшего значения хmах шкалы прибора составляет абсолютная приборная погрешность Δxпр. Таким образом
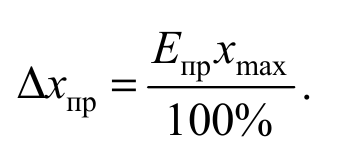
Формула O6
Обычно класс точности может принимать одно из семи значений: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Если на шкале прибора класс точности не указан, то это внеклассный прибор и его приведенная погрешность превышает 4%.
В предположении о независимости возникновения случайных и систематических погрешностей полная (суммарная) погрешность прямого измерения определяется по формуле
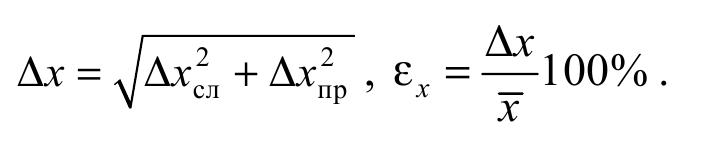
Формула O7
Если одна из погрешностей Δxсл или Δxпр в несколько раз (три или более) меньше другой, то вклад меньшей в полную погрешность оказывается незначительным и им можно пренебречь.
Пусть измеряемая физическая величина у не измеряется непосредственно прибором, а выражается по некоторой формуле через другие величины х1, х2, …, хm, значения которых получают в результате прямых измерений, т. е.
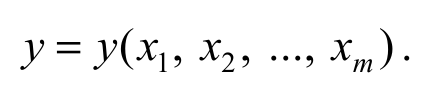
Формула O8
Наилучшая оценка y истинного значения величины y получается, если для ее расчета по формуле (О8) используются наилучшие оценки xk прямых измерений (k = 1, 2, …, m). Так, что
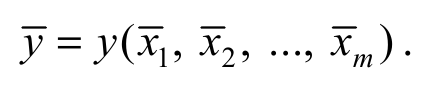
Формула O9
Поскольку все величины хk (k = 1, …, m) измерены с некоторыми погрешностями Δхk прямого измерения, то y также будет определена с некоторой погрешностью Δу, которая вычисляется по формуле
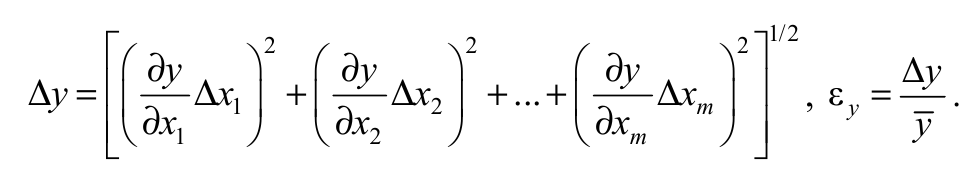
Формула O10
где ∂y / ∂xk − частные производные по переменным xk, вычисленные при x1=x1,x2=x2, ..., xm=xm.
Результат прямого или косвенного измерения величины х представляет собой приближенное число, точность которого определяется погрешностью измерений. Поэтому результаты измерения принято приводить интервалом, в котором с установленной вероятностью может находиться измеряемая величина:
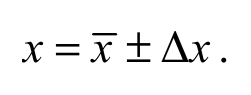
Формула O11
Значащими цифрами приближенного числа х называют все цифры этого числа, кроме нулей, стоящих впереди числа, а также нулей, поставленных в конце числа вместо цифр, отброшенных при округлении. Например, в числе 0,00308 три значащие цифры; в числе 6700, полученном при округлении числа 6698, две значащие цифры. Заметим, что в конце числа могут быть и значащие нули. При этом записи чисел 2,7 и 2,70 отличаются друг от друга. Запись 2,7 означает, что верны только цифры целых и десятых. Запись 2,70 означает, что верны и сотые доли.
Для того чтобы числа не содержали незначащих нулей, их принято записывать в показательной форме с запятой после первой значащей цифры. Например: 0,00308 = 3,08 · 10–3; 6700 = 6,7 · 103. Значащие нули в конце приближенного числа при такой записи не отбрасываются, например х = 1 т = 1000 кг = 1,000· 103 кг.
Округление результатов измерений следует начинать с погрешности. Найденные значения погрешностей также являются приближенными. В соответствии с точностью используемых методов обработки абсолютную погрешность Δx опытов округляют не более чем до двух первых значащих цифр. Абсолютную погрешность, начинающуюся с единицы, записывают двумя цифрами. При другой первой цифре указывается только одна цифра. Относительная погрешность ε округляется до первых двух значащих цифр.
После того, как погрешность записана, значение результата должно быть округлено таким образом, чтобы его последняя значащая цифра была того же разряда, что и у погрешности. Примеры правильно записанных результатов измерений: l = (68,0 ± 0,5) см; t = (1,67 ± 0,14) · 103 с; υ = (12,48 ± 0,04) м/с.
Если данное число является промежуточным и будет использоваться в других вычислениях, то в нем, как и в его погрешности, сохраняют лишний разряд, чтобы не накапливать погрешность за счет округлений.