



Механические колебания, распространяющиеся в упругой среде (твердой, жидкой или газообразной), называются механическими или упругими волнами.
Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение. Они лишь совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.
Упругая волна называется продольной, если колебания частиц среды происходят в направлении распространения волны. Продольные волны связаны с объемной деформацией растяжения − сжатия среды, поэтому они могут распространяться как в твердых телах, так и в жидкостях и газообразных средах.
 Упругая волна называется поперечной, если колебания частиц среды происходят в плоскостях, перпендикулярных к направлению распространения волны Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела.
Упругая волна называется поперечной, если колебания частиц среды происходят в плоскостях, перпендикулярных к направлению распространения волны Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела.
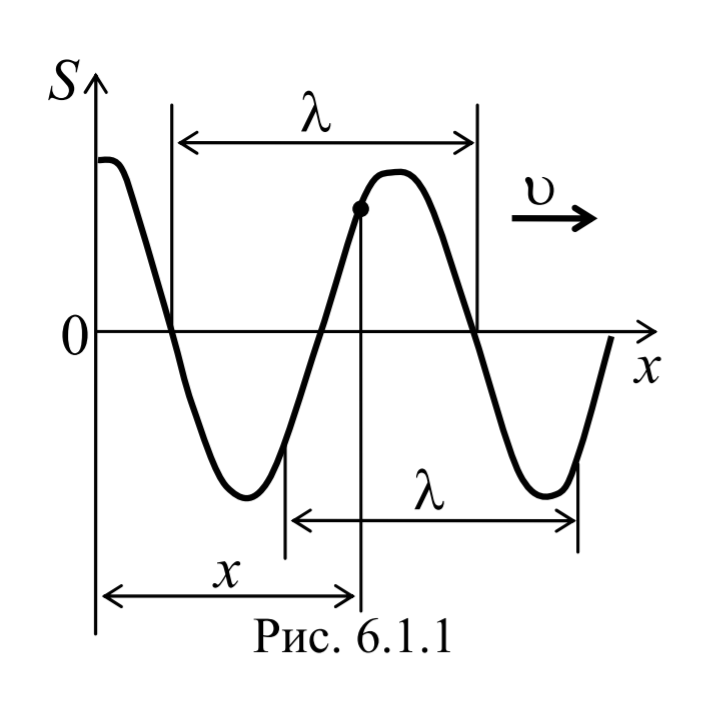
На рис. 6.1.1 представлена гармоническая поперечная волна, распространяющаяся вдоль оси 0х. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны. Длина волны также равна тому расстоянию, на которое распространяется определенная фаза колебания за период колебаний

Формула 9.1.1
Колеблются не только частицы, расположенные вдоль оси 0х, а совокупность частиц, заключенных в некотором объеме. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны. Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, а в сферической − множество концентрических сфер.
Уравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t
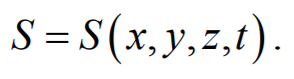
Формула 6.2.1
Эта функция должна быть периодической как относительно времени t, так и относительно координат x, y, z. Периодичность по времени вытекает из того, что смещение S описывает колебания частицы с координатами x, y, z, а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.
Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t
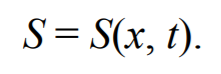
Формула 6.2.2
Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х. Пусть колебания точек, лежащих в плоскости х = 0 имеют вид
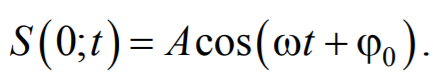
Формула 6.2.3
Найдем вид колебания точек в плоскости, соответствующей произвольному значению х. Для того, чтобы пройти путь от плоскости х = 0 до плоскости х, волне требуется время τ = x/υ. Следовательно, колебания частиц, лежащих в плоскости х, будут отставать по времени на τ от колебаний частиц в плоскости х = 0 и описываться уравнением
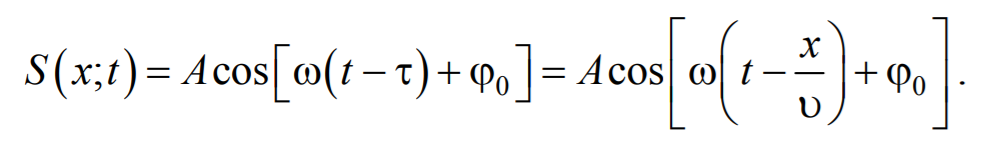
Формула 6.2.4
где А − амплитуда волны; ϕ0 − начальная фаза волны (определяется выбором начал отсчета х и t).
Зафиксируем какое-либо значение фазы ω(t-x/υ)+ϕ0=const. Это выражение определяет связь между временем t и тем местом х, в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим
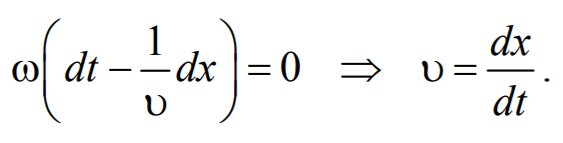
Формула 6.2.5
Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью.
При υ > 0 волна распространяется в сторону возрастания х. Волна, распространяющаяся в противоположном направлении, описывается уравнением

Формула 6.2.6
Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину $$k = {2π \over λ}$$, которая называется волновым числом, которое можно представить в виде 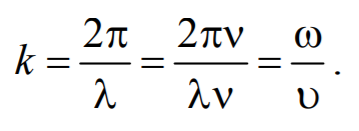
Формула 6.2.7
Тогда уравнение плоской волны будет иметь вид
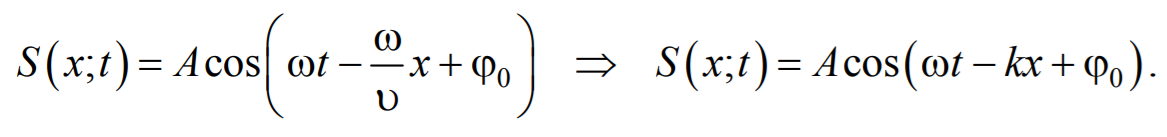
Формула 6.2.8
Мы предполагали, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону A=A0e−βx. Тогда уравнение плоской волны для поглощающей среды имеет вид
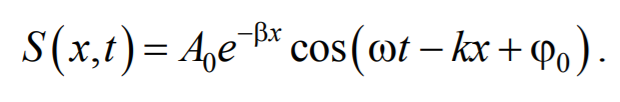
Формула 6.2.9
Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид 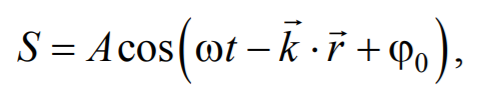
Формула 6.3.1
где r − радиус-вектор, точки волны; r=k×n − волновой вектор; n− единичный вектор нормали к волновой поверхности
Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.
Перейдем от радиус-вектора точки к ее координатам x, y, z 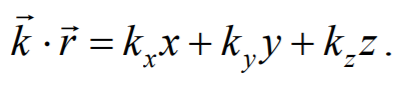 Тогда уравнение (6.3.2) примет вид
Тогда уравнение (6.3.2) примет вид
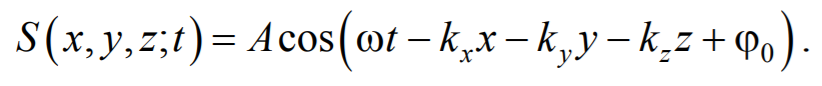
Формула 6.3.3
Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)
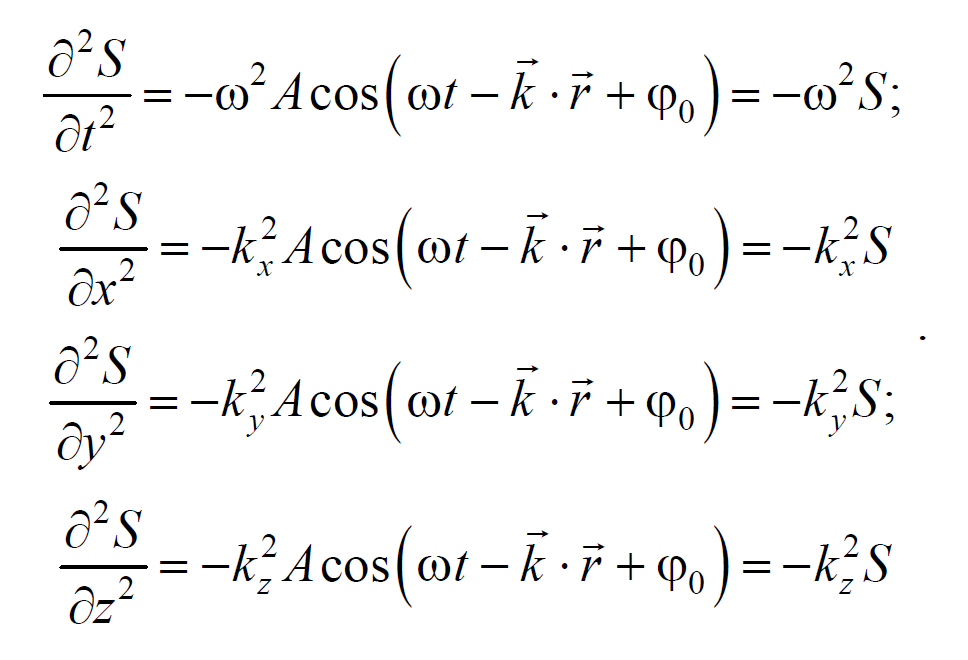
Формула 6.3.4
Сложив производные по координатам, и с учетом производной по времени, получим
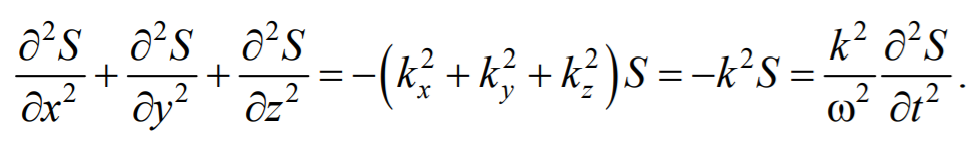
Формула 6.3.5
Произведем замену $${k^2 \over w^2}={w^2 \over v^2}{1^2 \over w^2}={1^2 \over v^2}$$ и получим волновое уравнение $${∂^2S \over ∂x^2}+{∂^2S \over ∂y^2}+{∂^2S \over ∂z^2}={1 \over v^2}{∂^2S \over ∂t^2}$$ или
Формула 6.3.4
где $$Δ={∂^2 \over ∂x^2}+{∂^2 \over ∂y^2}+{∂^2 \over ∂z^2}$$ − оператор Лапласа.
Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х. Выделим в среде цилиндрический объем с площадью основания S0 и высотой dx. Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S, то смещение основания с координатой x+dx будет S+dS. Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию ε=∂S/∂x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения σ, которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия 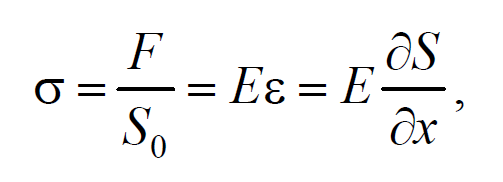
Формула 6.4.1
где Е − модуль Юнга среды.
Из зависимости смещения от координаты x видно, что относительная деформация ∂S/∂x, а также, и напряжение σ в фиксированный момент времени зависят от х. В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.
Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема 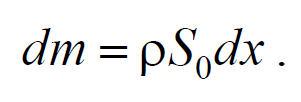
Формула 6.4.2
где ρ − плотность недеформированной среды.Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным
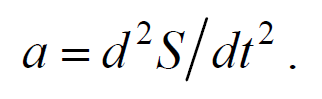
Формула 6.4.3
Тогда этот участок объема будет растянут под влиянием сил F1 и F2, приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно
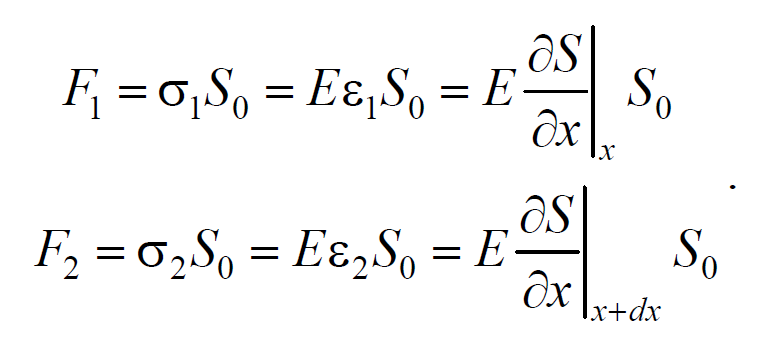
Формула 6.4.4
После разложения силы F2 в ряд, получим
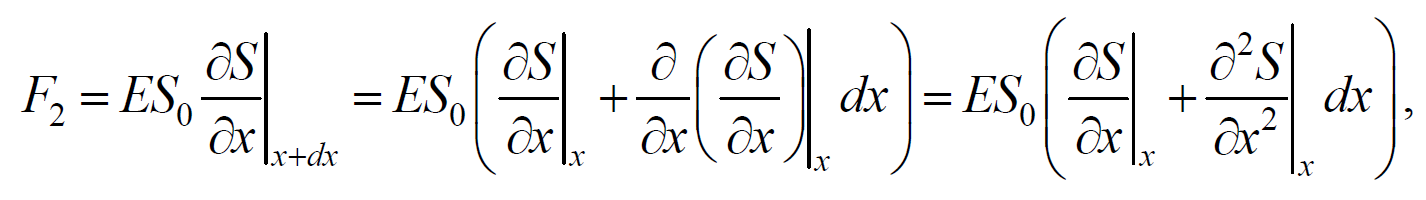
Формула 6.4.5
и результирующая F1, F2 сил, действующая на элемент объема равна
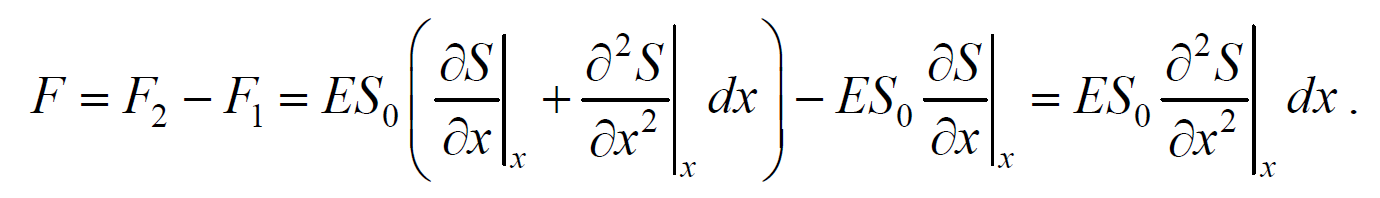
Формула 6.4.6
Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим 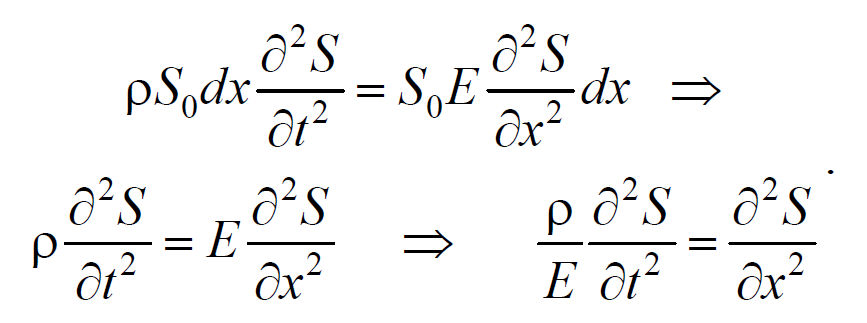
Формула 6.4.7
Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) $${∂^2S \over ∂x^2}={1 \over v^2}{∂^2S \over ∂t^2}$$ , получим 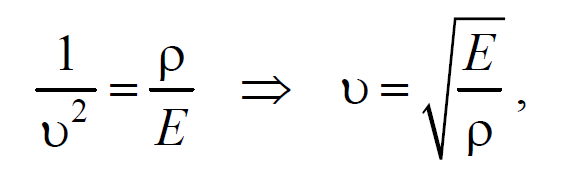
Формула 6.4.8
где Е − модуль Юнга.
Полученное уравнение определяет фазовую скорость продольных упругих волн.
Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид 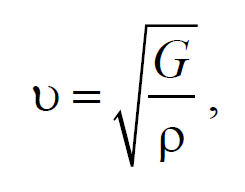
Формула 6.4.9
где G − модуль сдвига.