



Кинематика (от греч. движение) − раздел механики, посвященный изучению движения материальных объектов без учета их масс и действующих на них сил, т. е. кинематика рассматривает движение без учета причин, его вызывающих. Устанавливаемые здесь закономерности используются при кинематических исследованиях движений, в частности, при расчете механических передач в различных технических устройствах, а также при решении задач динамики.
Основной задачей кинематики является расчет кинематических характеристик движущихся объектов, к которым относятся скорость, ускорение и траектория.
В зависимости от изучаемого объекта выделяют кинематику материальной точки, твердого тела и непрерывно распределенной среды (деформируемого твердого тела, жидкости, газа).
Для описания движения необходимо выбрать систему отсчета.
Система отсчета состоит из тела отсчета и системы пространственных координат, снабженной часами и связанной с телом отсчета.
Тело отсчета − произвольно выбранное, в идеале − абсолютнотвердое тело, относительно которого определяется положение остальных тел.
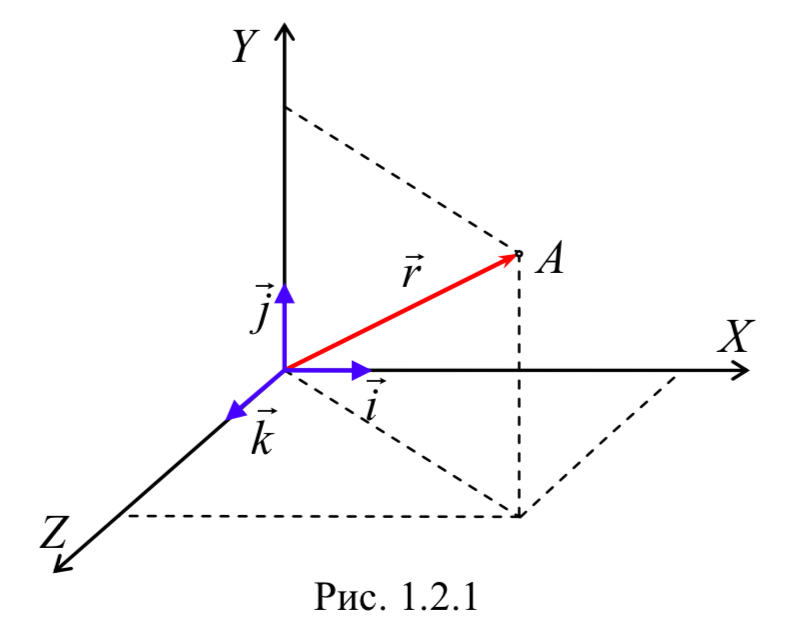
При векторном способе задания движения положение материальной точки в данный момент времени характеризуется радиус-вектором r, проведенным из начала координат в данную точку (рис. 1.2.1).
r=x(t)i+y(t)j+z(t)k
При движении материальной точки конец радиус-вектора описывает в пространстве кривую, которая называется траекторией движущейся точки. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Длина и направление радиус-вектора изменяется со временем согласно некоторому закону r = r (t), который называется уравнением движения материальной точки.
При координатном способе задания движения используется декартова система координат. Положение материальной точки в данный момент времени характеризуется тремя координатами X, Y и Z, а перемещение может быть представлено как результат трех независимых перемещений вдоль координатных осей: x=x(t), y=y(t), z=z(t).
Для характеристики движения вводится понятие вектора скорости, который определяет как быстроту движения, так и направление в данный момент времени.
Средней скоростью на некотором участке MN называется величина равная отношению перемещения Δr к промежутку времени Δt, за который это перемещение произошло
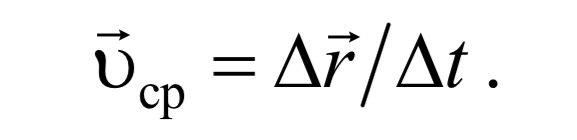
Формула 1.3.1
Вектор мгновенной скорости есть предел, к которому стремится вектор υср пристремлении Δt0, т.е.
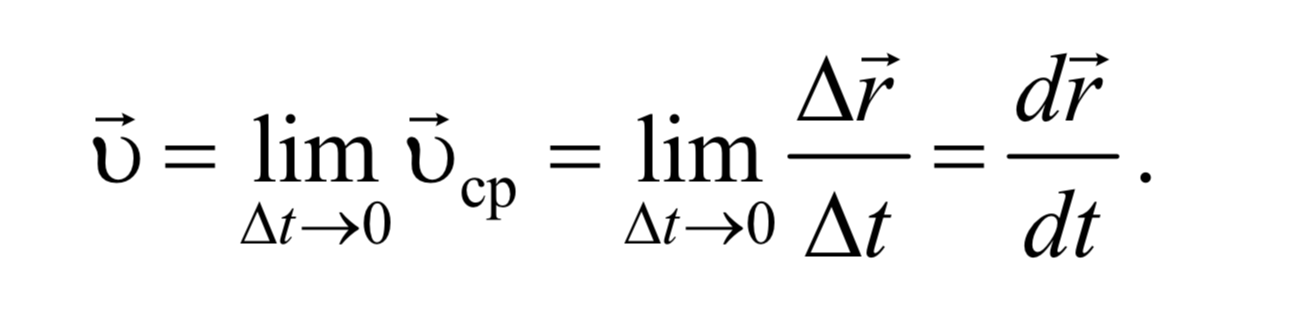
Формула 1.3.2
При Δt0 направление вектора Δr стремится к касательной к траектории в точке 1.
Кроме того, что при Δt0 |Δr| Δs поэтому модуль скорости |υ| равен
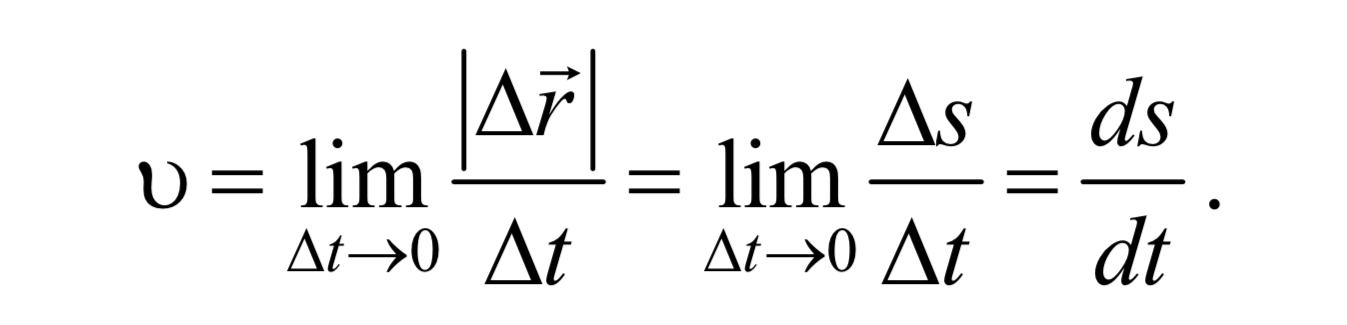
Формула 1.3.3
В декартовых координатах
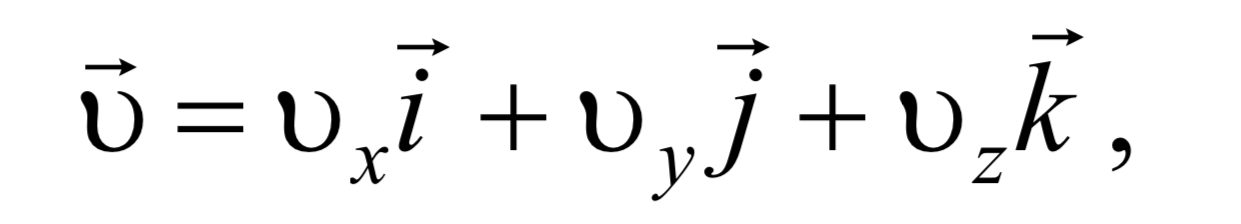
Формула 1.3.4
где
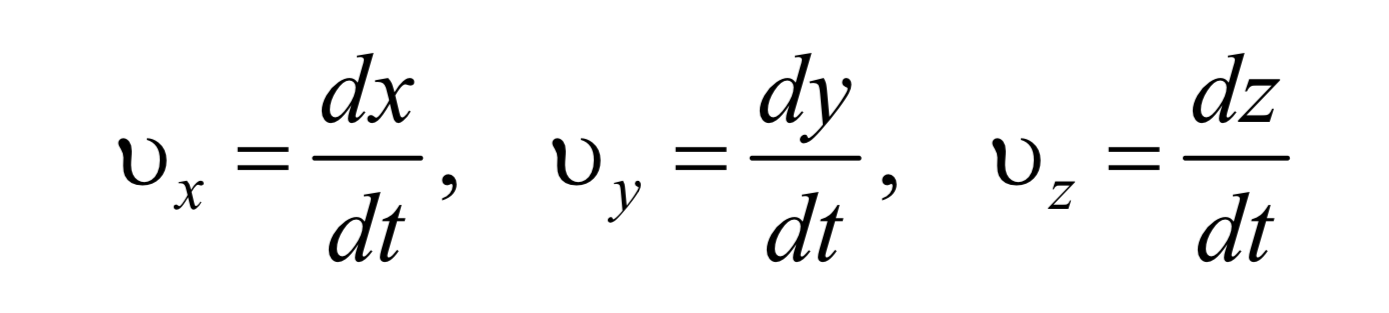
Формула 1.3.5
есть проекции скорости υ на оси х, y,z. Модуль скорости
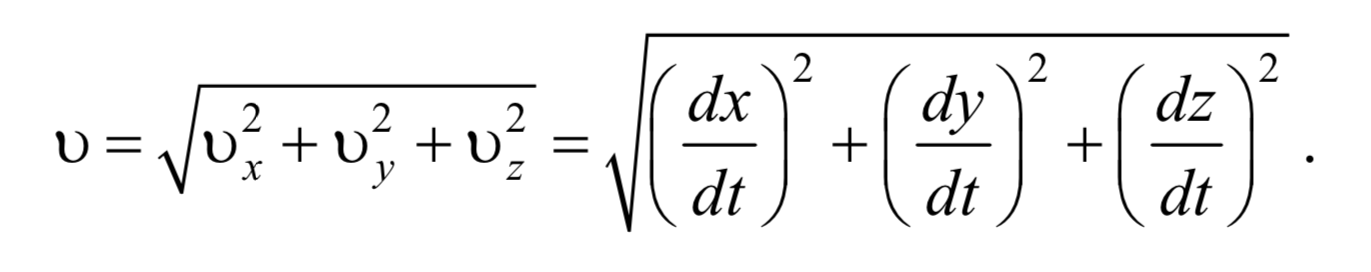
Формула 1.3.6
Быстрота изменения скорости со временем характеризуется ускорением. Ускорение равно первой производной от вектора скорости υ или второй производной от радиус-вектора r(t) по времени. Ускорение − это векторная величина
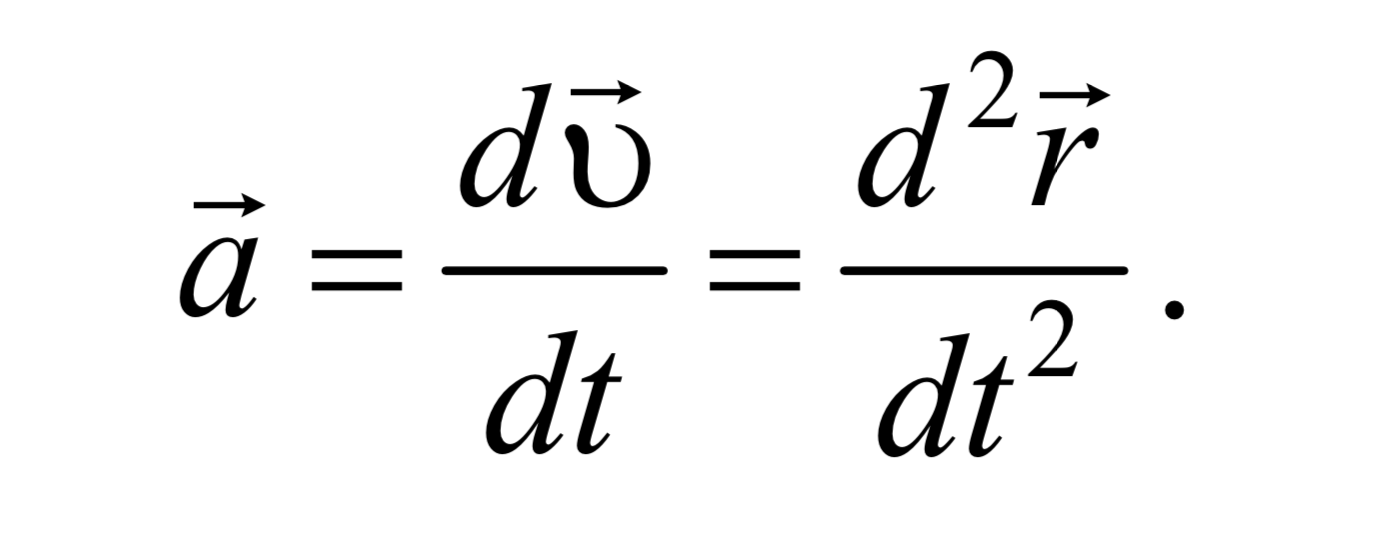
Формула 1.3.7
Ускорение можно найти по его проекциям на оси координат
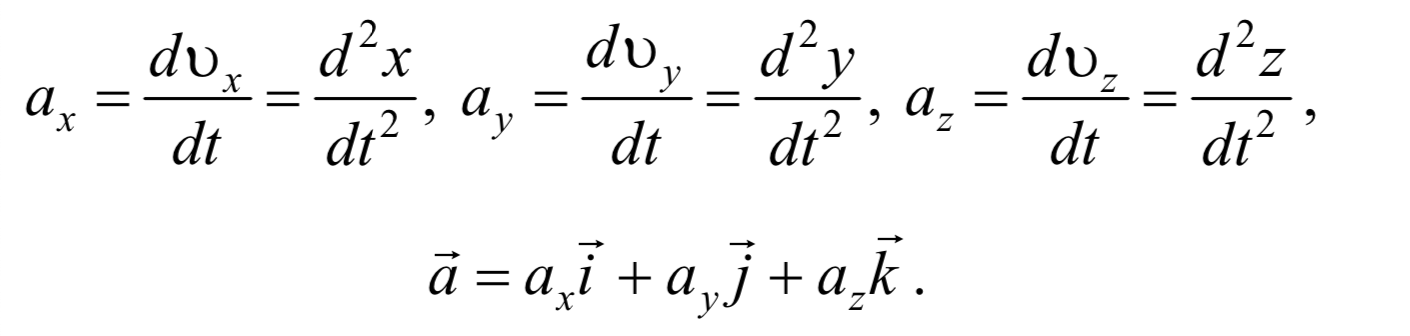
Формула 1.3.8 и 1.3.9
Модуль
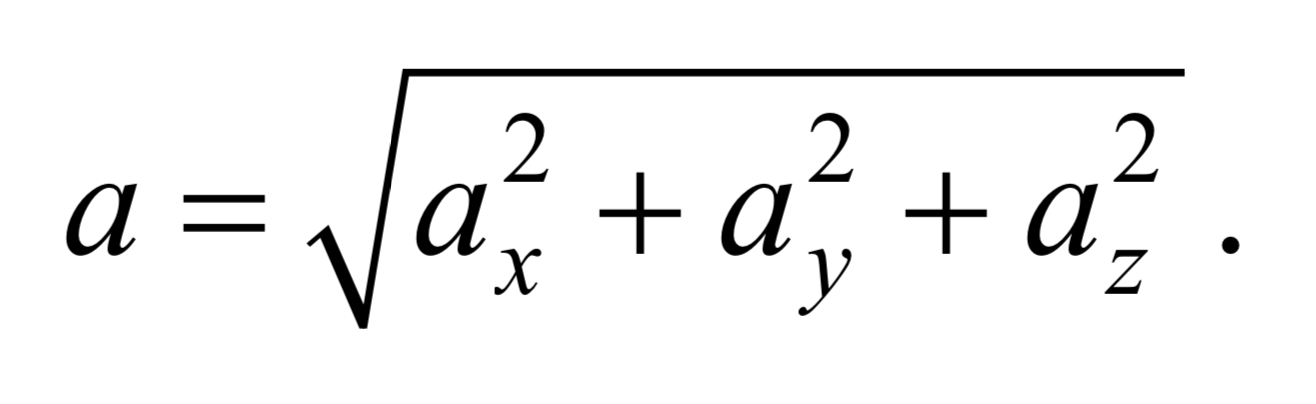
Формула 1.3.10