Лекция №2. Элементы кинематики

В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.

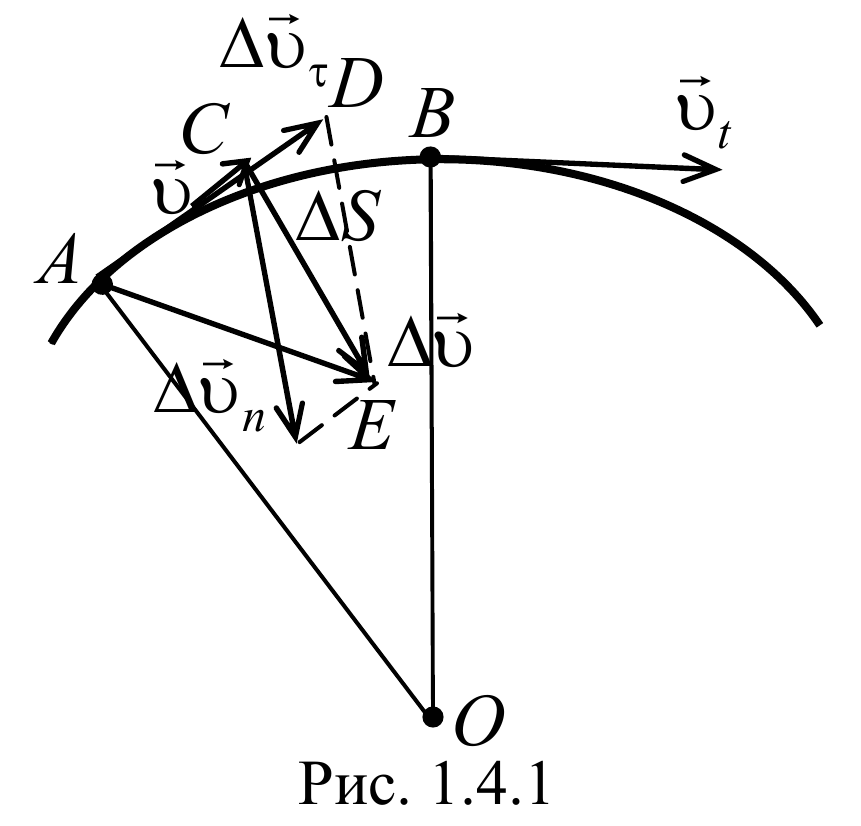
Рассмотрим плоское движение, т. е. такое, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор υ задает скорость точки А, в момент времени t. За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от υ как по модулю, так и направлению и равную υ₁=υ+Δυ. Перенесем вектор υ₁ в точку А и найдем Δυ (рис.). Средним ускорением a_ср неравномерного движения в интервале времени от t до t+Δt называется векторная величина, равная отношению изменения скорости Δυ к интервалу времени Δt:

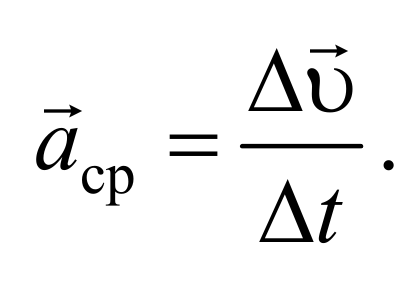
Формула 1.4.1

Ускорение в данный момент времени (мгновенное ускорение) представляет собой предел, к которому стремится выражение (1.4.1) при Δt0, т. е.

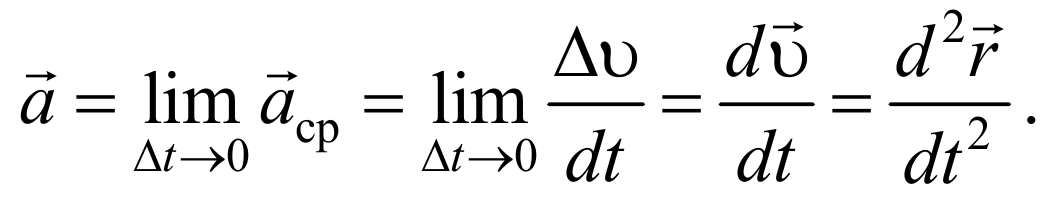
Формула 1.4.2

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

Разложим вектор Δυ на две составляющие. Для этого из точки А (рис. 1.4.1) по направлению скорости υ отложим вектор AD , по модулю равный υ₁. Очевидно, что вектор CD , равный Δυ_τ, определяет изменение скорости по модулю за время Δt: Δυ_τ=υ₁−υ. Вторая же составляющая Δυ_n вектора Δυ характеризует изменение скорости за время Δt no направлению.

Тангенциальная составляющая ускорения

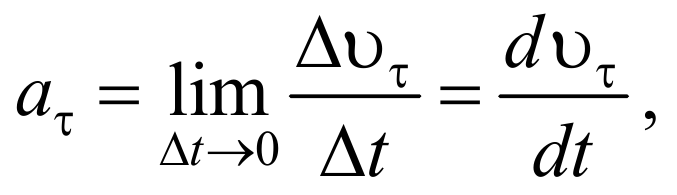
Формула 1.4.3

т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Определим вторую составляющую ускорения. Допустим, что точка B близка к точке A, поэтому Δs можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды AB. Тогда из подобия треугольников AOB и EAD следует Δυ_n/AB=υ₁/r, но так как AB=υΔt, то Δυ_n/t=υυ₁/r. В пределе Δt0, получим υ₁υ.

Поскольку υ₁υ, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол АDE между υ и Δυ_n стремится к прямому. Следовательно, при Δt0 векторы υ и Δυ_nоказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Δυ_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

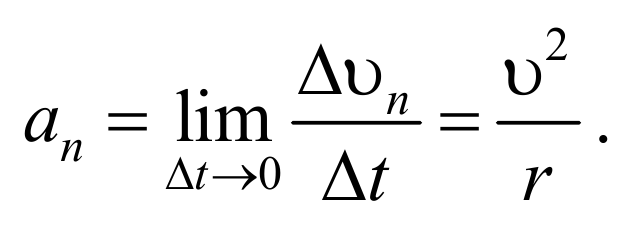
Формула 1.4.4

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.

Таким образом, полное ускорение тела a есть геометрическая сумма тангенциальной a_τ и нормальной a_n составляющих

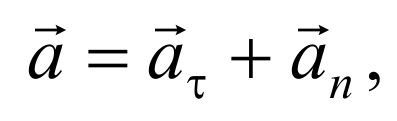
Формула 1.4.5

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.

Векторы a_τ и a_n взаимно перпендикулярны поэтому модуль полного ускорения равен

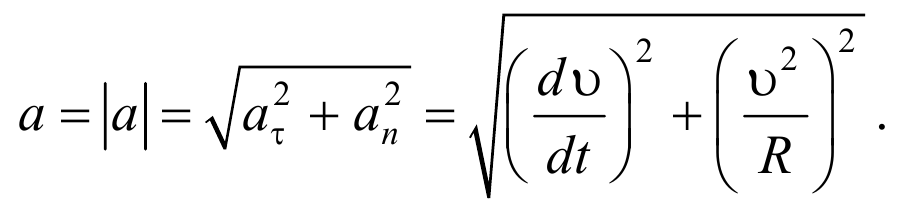
Формула 1.4.6

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1) a_τ=0,a_n=0 - прямолинейное равномерное движение.

2) a_τ=const,a_n=0 - прямолинейное равнопеременное движение.

При таком движении $$\vec{a}_τ = \vec{a} = {d\vec{υ} \over dt}$$ то, проинтегрировав это выражение, получим:

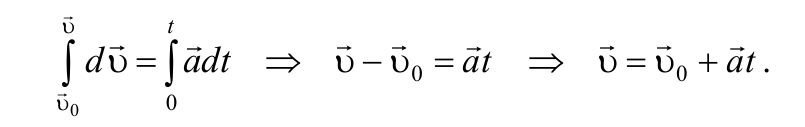
Так как $$\vec{υ} = {d\vec{r} \over dt}$$, то, проинтегрировав полученное выражение в пределах от нуля до произвольного момента времени можно найти перемещение точк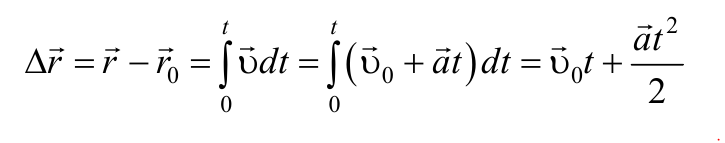и: или

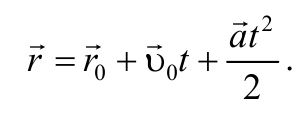
3) a_τ= ƒ(t), a_n=0 − прямолинейное движение с переменным ускорением.

4) a_τ=0, a_n=const - При таком движении скорость точки не изменяется по модулю, так как тангенциальная составляющая равна нулю, а изменяется только по направлению.

5) a_τ=const, a_n≠const − равнопеременное движение по окружности.

6) a_τ=0, a_n≠0 − равномерное криволинейное движение.

7) a_τ=const, a_n≠0 − криволинейное равнопеременное движение.

Вращательное движение − это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. При вращательном движении скорости и ускорения различных точек тела неодинаковы. Поэтому в качестве общих кинематических характеристик движения тела при вращении вводятся угол поворота, угловая скорость и угловое ускорение тела. При вращении тела угол поворота изменяется со временем по некоторому закону ϕ = ϕ(t), который называется уравнением вращательного движения тела.

Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:

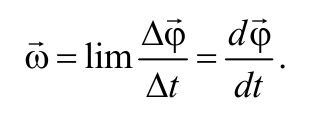
Формула 1.6.1

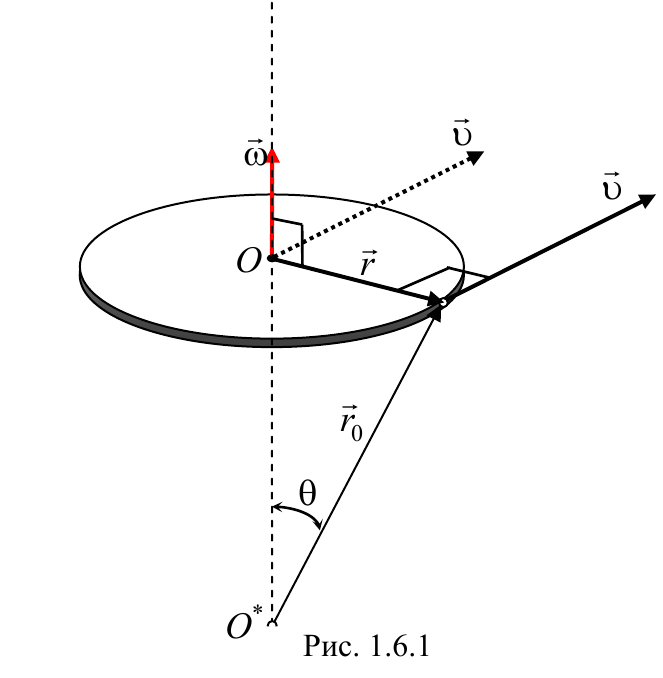
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.

Скорость произвольной точки вращающегося тела называется линейной скоростьюэтой точки.

При равномерном вращении угловая скорость не изменяется со временем, то есть является постоянной величиной (ω = const). Тогда

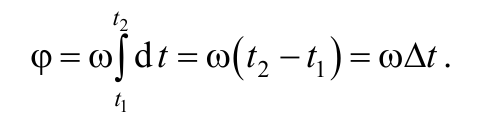
Равномерное вращение характеризуется периодом вращения и частотой вращения.

Период вращения − это время, за которое точка совершает один полный оборот, т. е. поворачивается на угол ϕ = 2π и на основании выражения (1.6.1) $${T} = {2{π} \over ω}$$

Частота вращения − это число полных оборотов, которое делает точка при равномерном вращении, за единицу времени: $${n} = {1\over T} = {ω\over 2π}$$ , откуда ϕ = 2πn.

Для характеристики неравномерного вращения тела вводится понятие углового ускорения.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

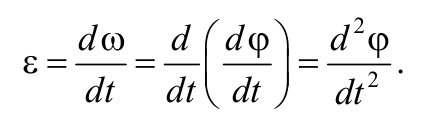
Формула 1.6.2

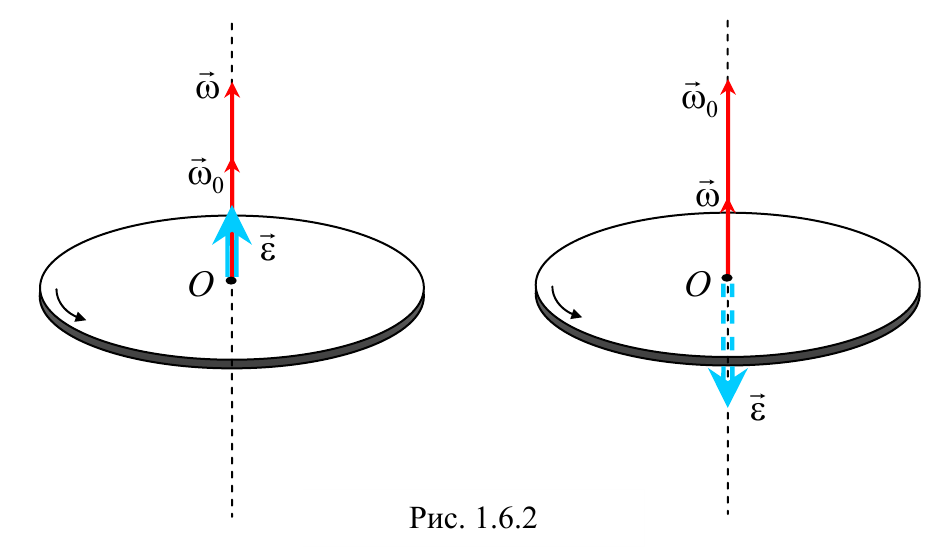
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

В случае равнопеременного движения точки по окружности (ε = const) угловая скорость определяется по формуле

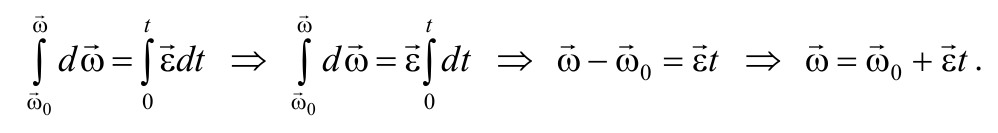
Формула 1.6.3

Или в скалярном виде

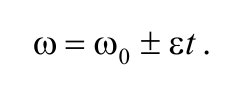
Формула 1.6.4

Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела

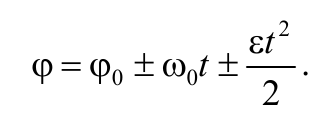
Формула 1.6.5

Исключив из последнего уравнения t, получим

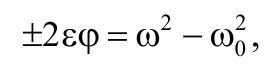
Формула 1.6.6

где φ = 2πN, N − число полное число оборотов, совершенных телом.

В случае ε = ε(t), угловая скорость и закон вращательного движения определяются следующими формулами

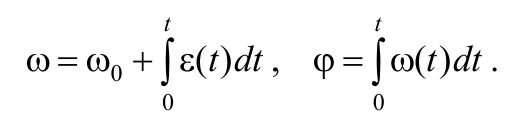
Формула 1.6.7

За время dt точка проходит по дуге окружности радиуса R путь dS = Rdφ . Поэтому $${υ} = {dS\over dt} = {R}{dφ\over dt} = {ωR}$$.

Если угол поворота вращающегося тела представить в виде dφ = ω(t)dt и проинтегрировать в пределах от начального момента времени t₁ до конечного момента времени t₂, то получится угол, на который совершила поворот тело за время:

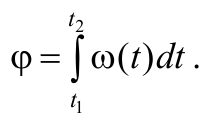
Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:

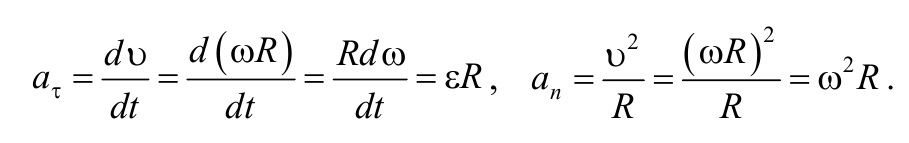
Формула 1.7.1

Полученные соотношения (1.7.1) можно записать в векторном виде. Для этого на оси вращения ОО* (рис. 1.6.1) тела выберем любую точку A и проведем из нее радиус-вектор r в точку M. Векторное произведение ω × r по модулю и направлению совпадает с вектором скорости υ точки M:

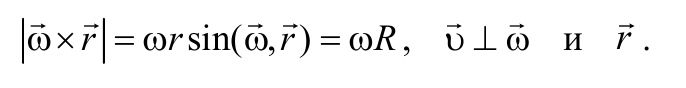
Формула 1.7.2

Следовательно, можно записать, что вектор скорости υ = ω × r, а вектор ускорения точки

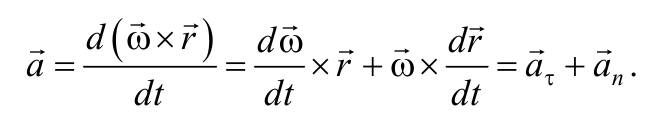
Формула 1.7.3

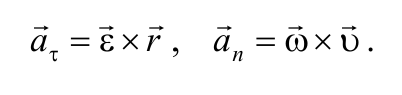
Формула 1.7.4