Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА

Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.

Разобьем твердое тело на элементарные массы m_i, тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы

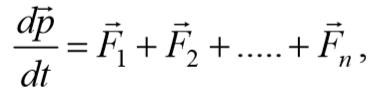
Формула 4.1.1

p=$${\sum_{i=1}^n}$$m_iυ_i=mυ_C - импульс всех материальных точек твердого тела.

Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс

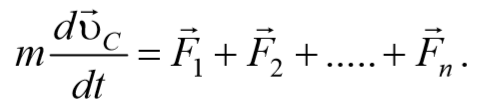
Формула 4.1.2

Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.

Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра

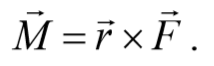
Формула 4.2.1

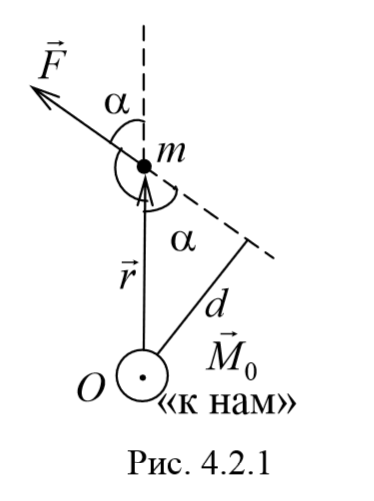
Пусть на частицу массой m действует сила F, а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F, и он перпендикулярен как вектору r, так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен

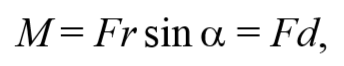
Формула 4.2.2

где d=r sin α − плечо силы относительно точки O.

Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.

Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F, действующей на твердое тело, на плечо силы d относительно этой оси.

Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:

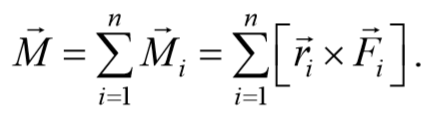
Формула 4.2.3

Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс mυ называется моментом импульса материальной точки относительно некоторого центра

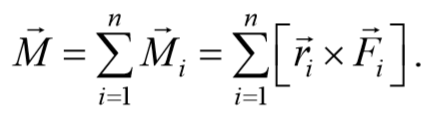
Формула 4.2.4

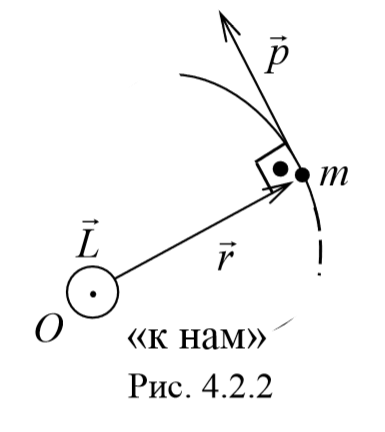
Пусть частица массой m имеет импульс p, а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p, и он перпендикулярен как вектору r, так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен

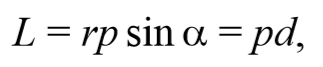
Формула 4.2.5

где d − плечо импульса относительно точки O.

Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.

Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.

Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы

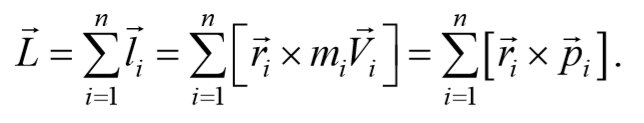
Формула 4.2.6

Рассмотрим систему материальных точек массами m₁, m₂, ..., m_n движущихся со скоростями υ₁, υ₂, ..., υ_n. Пусть на каждую из этих точек действуют: равнодействующие внутренних сил Fⁱ₁, Fⁱ₂, ..., Fⁱ_n, и равнодействующие внешних сил F^e₁, F^e₂, ..., F^e_n.

Запишем уравнения движения частиц:

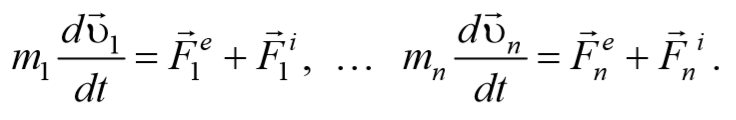
Формула 4.3.3

Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим

.........,

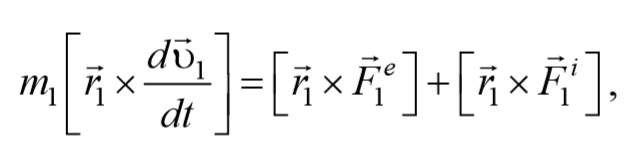
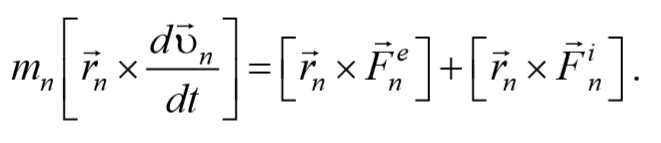
Формула 4.3.4

Преобразуем данные уравнения

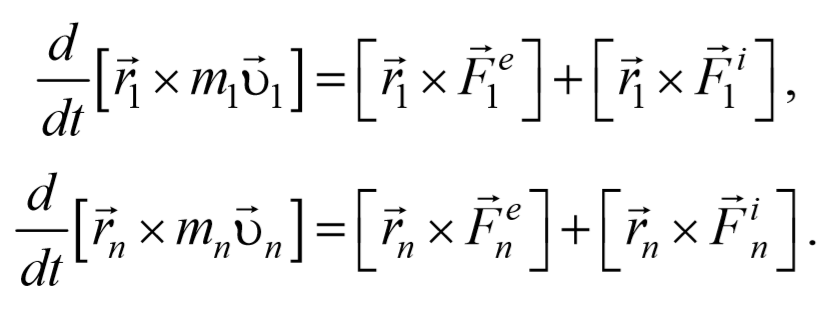
Формула 4.3.5

Сложим эти уравнения и получим

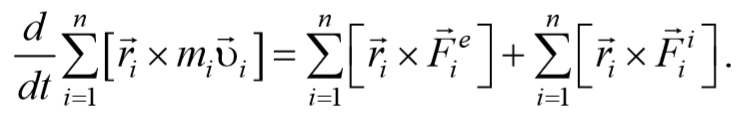
Формула 4.3.6

В последнем уравнении:

$${\sum_{i=1}^n}$$[r_i×m_iυ_i]=dL/dt - есть момент импульса системы,

$${\sum_{i=1}^n}$$[r_i×Fⁱ_i]=∑ⁿ_i=1Mⁱ_i - сумма моментов внутренних сил,

$${\sum_{i=1}^n}$$[r_i×F^e_i]=∑ⁿ_i=1M^e_i - сумма моментов внешних сил.

Таким образом, выражение (4.3.6) можно записать в виде

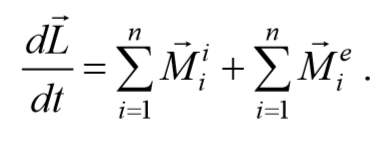
Формула 4.3.7

Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $${\sum_{i=1}^n}$$Mⁱ_i=0, получим основное уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы).

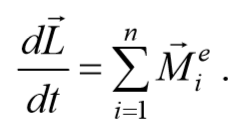
Формула 4.3.8

Если момент внешних сил $${\sum_{i=1}^n}$$M^e_i=0, то получим

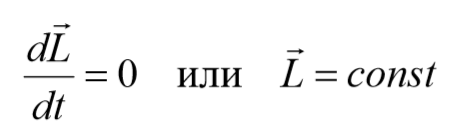
Формула 4.4.1

закон сохранения момента импульса.

Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.

Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.

Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.

Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:

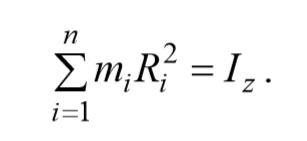
Формула 4.5.1

Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м².

Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.

Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:

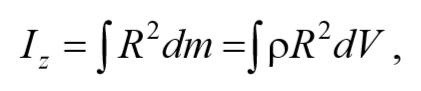
Формула 4.5.2

где R − расстояние от элементарной массы dm до оси вращения.

Существуют два свойства момента инерции:

1) Теорема Штейнера: момент инерции тела I_z относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

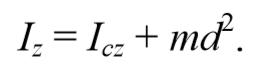
Формула 4.6.1

2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:

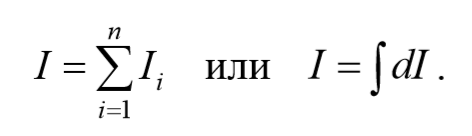
Формула 4.6.2