



Упругая волна – это процесс распространения колебаний частиц сплошной среды (от источника вдоль луча волны). В зависимости от вида фронта волны различают плоские и сферические волны (см. лаб. раб. № 11).
Продольными называются волны, в которых частицы среды совершают колебания в направлении распространения волны, т. е. вдоль луча волны.
Поперечными называются волны, в которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны, т. е. перпендикулярно лучу волны.
Волновое уравнение является дифференциальным уравнением второго порядка в частных производных, т. е.
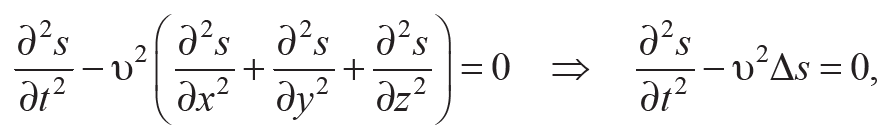
Формула 10.1
где s(x, y, z, t) – смещение частицы среды в момент времени t от ее положения в состоянии равновесия, т. е. смещения частиц зависят от их координат в положении равновесия и времени; ν – фазовая скорость волны; Δ=∂2s/∂x2+∂2s/∂y2+∂2s/∂z2 – оператор Лапласа.
В случае плоской волны, распространяющейся вдоль оси х, смещение s зависит от х и t. Тогда волновое уравнение (10.1) упрощается и имеет следующий вид:
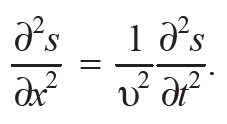
Формула 10.2
Решение этого дифференциального уравнения является уравнением плоской бегущей волны:
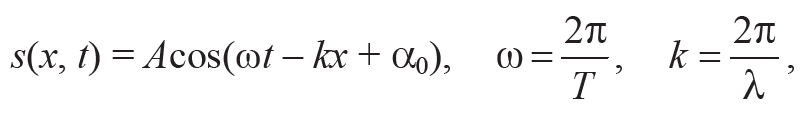
Формула 10.3
где А – амплитуда незатухающей волны; Т – период колебаний; ω = 2πν – циклическая частота (ν = 1 / Т); k = 2π / λ – волновое число; λ = νТ – длина волны; α0 – начальная фаза, а φ = ωt – kx + α0 – фаза волны в точке с координатой x в момент времени t.
Скорость ν распространения волны, т. е. скорость перемещения плоского фронта волны, называется фазовой скоростью, так как все точки плоского фронта имеют одинаковую фазу (ω / k = λ / T = ν).
В случае сферической волны решение волнового уравнения (10.1) имеет следующий вид:
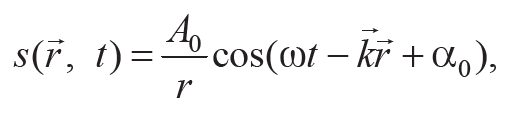
Формула 10.4
где k – волновой вектор, направленный в сторону распространения волны (модуль вектора k является волновым числом); kr – скалярное произведение векторов k и r.
Если волна, распространяющаяся в упругой среде, достигает границы раздела с другой средой, то она, преломляясь, продолжает распространяться в этой среде и частично отражается от границы. На рис. 10.1 изображен процесс отражении волны при ее нормальном падении, т. е. вектор ν фазовой скорости перпендикулярен плоской границе двух сред.
Оказывается, что при отражении волны не изменяются ни направление колебаний частиц среды, ни частота их колебаний. При отражении от менее плотной среды фаза колебаний тоже не изменяется, т. е. Δφ = 0 (рис. 10.1, а). При отражении от более плотной среды фаза колебаний скачком изменяется на противоположную, т. е. на Δφ = π. Происходит потеря полуволны (рис. 10.1, б).
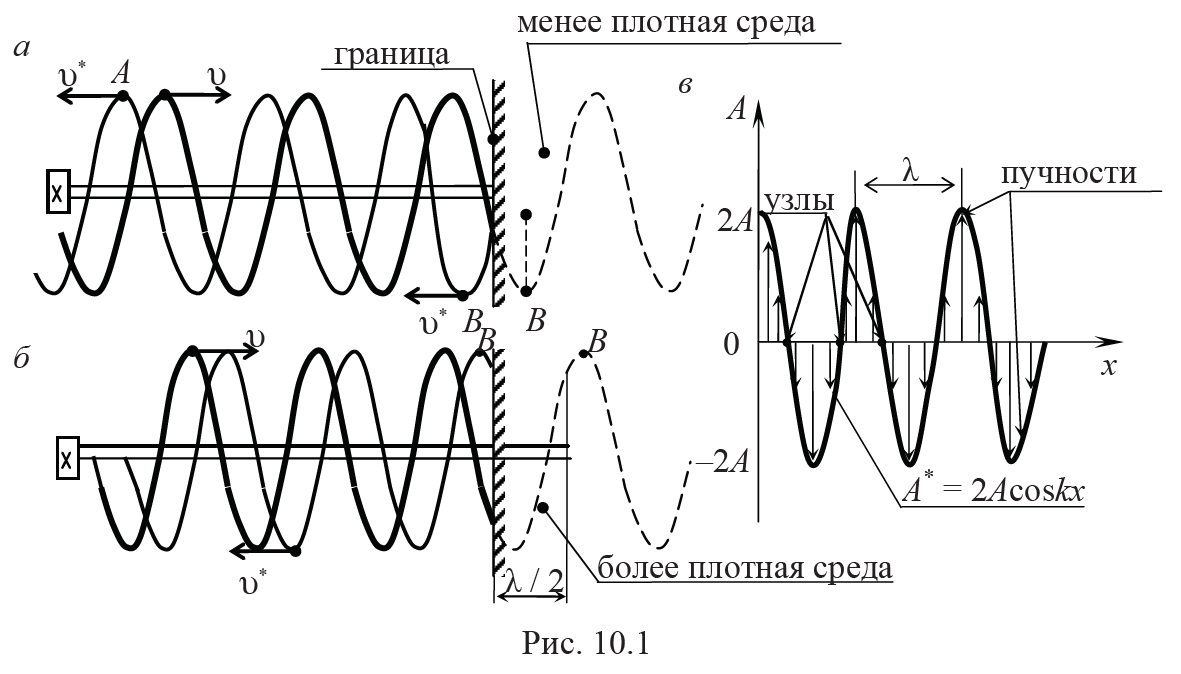
Отраженная волна распространяется навстречу падающей и при полном отражении (без потери энергии) их амплитуды будут равными.
Пусть уравнение s1(x, t) = Acos(ωt – kx) определяет плоскую падающую волну, которая распространяется вдоль оси х, тогда для отраженной волны с волновым вектором k*=-k получим уравнение s2(x, t) = Acos(ωt + kx). Результирующее смещение частиц среды, участвующих одновременно в двух колебаниях, определим с помощью принципа суперпозиции, т. е.
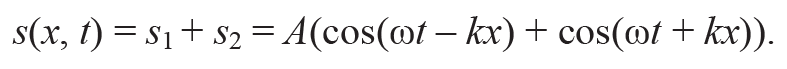
Формула 10.5
Воспользовавшись формулой суммы косинусов двух углов cosα + cosβ = 2cos((α +β)/ 2)cos((α −β)/ 2), получим уравнение стоячей волны:
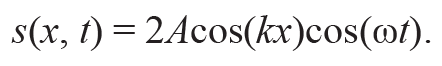
Формула 10.6
Последнее уравнение можно рассматривать как уравнение колебаний частиц среды, которые происходят с амплитудами, равными A* = 2A|cos(kx)| и, следовательно, зависящими от координаты x, т. е. от положения частицы на оси х. Множитель 2Acos(kx) в формуле (10.6) называется амплитудой стоячей волны (рис. 10.1, в). Термин стоячая волна отражает тот факт, что в процессе колебаний частиц среды положения максимумов и минимумов амплитуды (пучностей), а также ее узлов не изменяются во времени, т. е. они находятся на одном и том же месте. Координаты пучностей и узлов определяются следующими соотношениями (k = 2π / λ):
а) для пучностей
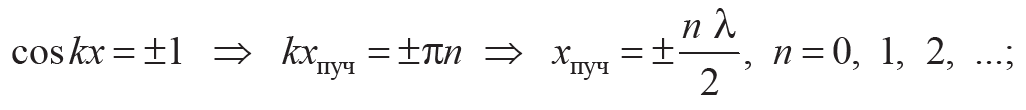
Формула 10.7
б) для узлов
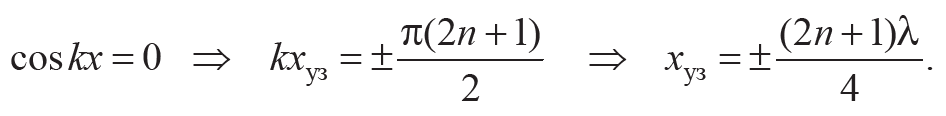
Формула 10.8
Расстояние между соседними узлами или соседними пучностями (максимумом и минимумом), равное λ / 2, называется длиной стоячей волны. Амплитуда A* стоячей волны зависит от координаты х, принимая положительные и отрицательные значения. Это означает, что частицы среды, находящиеся по разные стороны от какого-либо узла, колеблются в противофазе (рис. 10.1, в).
Из уравнений динамики колебательного движения частиц среды, которые получаются с помощью 2-го закона Ньютона, следует, что фазовые скорости волн выражаются через модуль Юнга Е и модуль сдвига G (см. лаб. раб. № 2):
а) для продольных волн скорость ν|| (рис. 10.2, а) рассчитывается по формуле
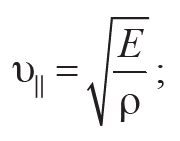
Формула 10.9
б) для поперечных волн скорость ν⊥ (рис. 10.2, б) рассчитывается по формуле
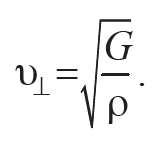
Формула 10.10
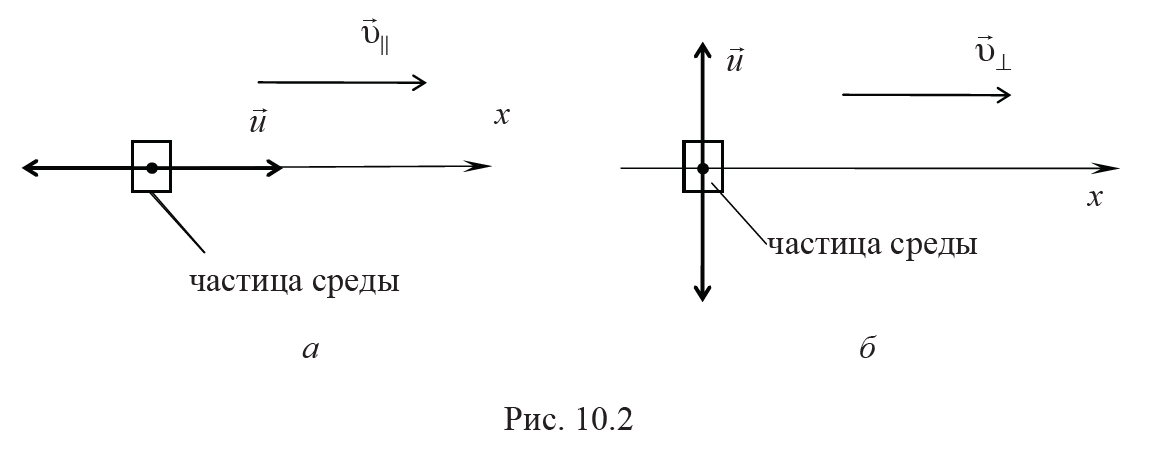
Продольные и поперечные волны могут распространяться в твердых телах, в которых возникают упругие силы при деформациях растяжения – сжатия (для продольных волн) и сдвига (для поперечных волн).
В жидкостях и газах упругие силы возникают при сжатии, поэтому возбуждаются только продольные волны, скорость которых рассчитывается по формуле
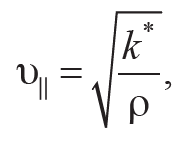
Формула 10.11
где k* – модуль объемного сжатия жидкости или газа.
Установка для исследования поперечных волн (рис. 10.3, а) состоит из металлической струны, один конец которой закреплен в точке А, а другой перекинут через легкий блок В. К концу струны прикреплена чашка D, нагружая которую гирями, можно изменять натяжение струны. Вдоль струны может перемещаться постоянный магнит М. Генератор переменного напряжения звуковой частоты (ЗГ) создает в струне переменный ток, сила которого I = I0cos(2πνt). Частоту ν тока в цепи можно изменять, вращая лимб 1 с делениями на передней панели ЗГ. На элемент струны длиной Δl с током I(t) (рис. 10.3, б), находящийся между полюсами магнита, действует переменная сила Ампера (FA = IBΔl), изменяющаяся с частотой ν. Вектор B индукции магнитного поля направлен от северного полюса N к южному полюсу S, поэтому он перпендикулярен линии АВ. Сила Ампера, действующая на участок Δl струны с переменным током I(t), направлена перпендикулярно вектору B(в соответствии с правилом левой руки, т. е. правилом векторного произведения: FA = IΔl × B). Под действием этой периодической силы участок струны длиной Δl начнет совершать вынужденные колебания, которые за счет сил упругости в струне будут распространяться вдоль струны от магнита М к ее концам А и В (поперечная волна). При отражении бегущих волн в точках А и В закрепления струны образуются отраженные волны, которые распространяются навстречу падающим и накладываются на них. При определенных частотах νn генератора (n = 1, 2, 3, …), совпадающих с собственными частотами струны, возникают устойчивые стоячие волны (с максимальной амплитудой, соответствующей явлению резонанса), причем точки закрепления струны А и В являются ее крайними узлами (рис. 10.3). В этом случае на струне длиной L укладывается целое число длин стоячих волн (λст = λ / 2), т. е. L = пλст = пλ / 2, где λ – длина бегущей волны.
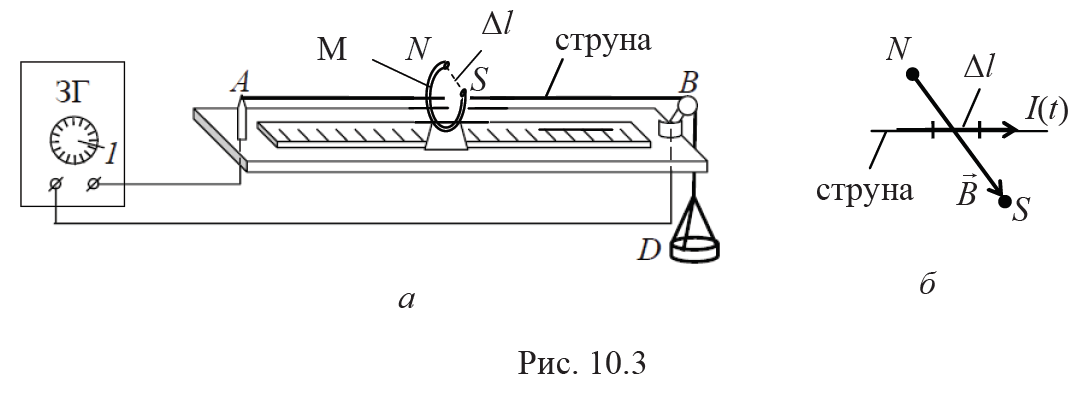
Используя соотношение λ = υТ = υ / ν, находим спектр собственных частот колебаний струны (L = nυ / (2ν)):
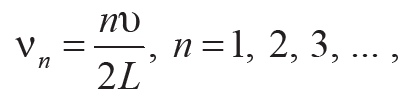
Формула 10.12
где υ – скорость распространения волны.
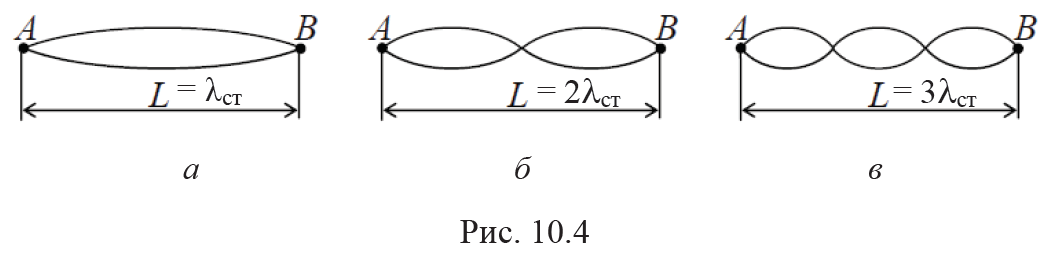
Наименьшую частоту ν1 = υ / (2L) (п = 1) называют основной частотой, или основным тоном, или первой гармоникой. В этом случае на струне укладывается одна длина стоячей волны (рис. 10.4, а), имеющей узлы в точках закрепления струны, а посередине пучность. При п = 2, 3, 4, ... имеют место обертоны, т. е. более высокие гармоники. При первом обертоне (n = 2) на длине струны укладываются две длины стоячей волны (рис. 10.4, б) и на струне имеются две пучности и три узла (два на концах струны и один посередине) и т. д. (рис. 10.4, в).
Из формулы (10.12) получается формула для косвенного измерения скорости распространения бегущей волны:
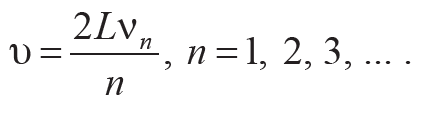
Формула 10.13
Эта скорость зависит от силы F натяжения струны:
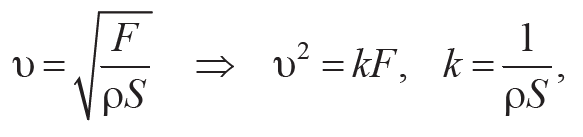
Формула 10.14
где ρ – плотность материала струны; S – площадь поперечного сечения струны.
Из (10.14) следует, что квадрат скорости волны прямо пропорционален силе F натяжения в используемой струне.
1. Подготовьте таблицу для занесения и обработки результатов измерений.
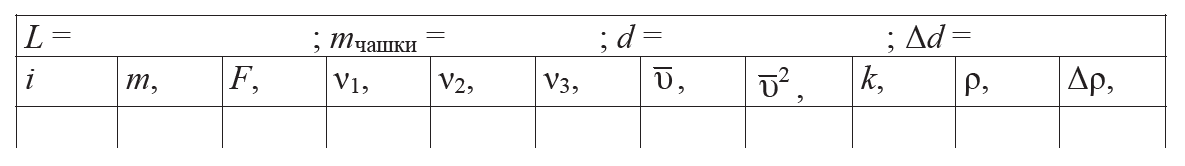
2. Измерьте с помощью микрометра диаметр d струны. Передвигая левую опору струны, установите длину L = 60 + 5n (в сантиметрах, n – номер Вашего звена в подгруппе) колеблющейся части струны. Постоянный магнит расположите на середине струны (область пучности при n = 1). На чашку D массой mч положите гирю массой mг = 100 г (тогда m = mч + mг, а сила натяжения струны F = mg).
3. С разрешения преподавателя включите ЗГ и после его прогрева ручкой «РЕГ. ВЫХОДА» установите на вольтметре максимальное значение напряжения.
4. Плавно увеличивая частоту ЗГ, добейтесь устойчивых вынужденных колебаний струны для основного тона (n = 1) и по лимбу ЗГ определите частоту ν1. При этом колеблющаяся струна будет иметь вид, показанный на рис. 10.5, а, а амплитуда колебаний должна быть максимальной (условия резонанса). Если струна ударяется о магнит, сместите его ближе к узлу.
5. Увеличивая частоту ЗГ, определите частоты первого ν2 и второго ν3 обертонов. При этом колебания струны будут иметь вид, показанный на рис. 10.5, б и 10.5, в соответственно, поэтому каждый раз магнит располагайте в области образования пучностей.
6. Проделайте аналогичные измерения (пункты 4, 5) при других нагрузках, используя гири с массами (mг = 150, 200, 250, 300, 350 г).
7. По формуле (10.12) для каждой нагрузки рассчитайте скорости ν1, ν2, ν3 и найдите их среднее значение ν.
8. Постройте график зависимости ν2 от F, откладывая по горизонтальной оси значение силы F, а по вертикальной – ν2. Убедитесь в линейной зависимости ν2 от F (в пределах погрешностей), как это следует из формулы (10.14).
9. Используя средние значения ν2 из формулы ν2 = kF вычислите коэффициент k при всех нагрузках. По формулам (О3) и (О4) определите среднее значение k и его случайную погрешность Δk.
10. Используя среднее значение коэффициента k, вычислите плотность ρ материала струны по формуле, вытекающей из выражения (10.14):
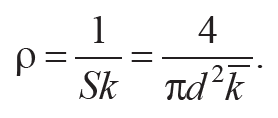
Формула 10.15
11. Погрешность косвенного измерения плотности ρ по формуле (10.15) определяется погрешностями измерения диаметра проволоки Δd и коэффициента Δk. Соотношения для расчета относительной ε и абсолютной Δρ погрешностей следуют из (О10):
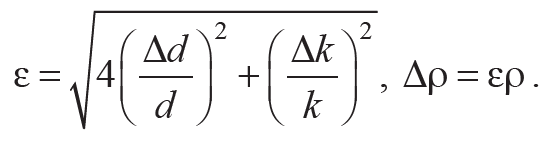
Формула 10.16
12. Вычислите относительную ε и абсолютную Δρ погрешности измерения плотности.
13. Подготовьте выводы по выполненной лабораторной работе.