Периодический процесс, в котором какая-либо физическая величина принимает одинаковые значения через равные промежутки времени, называется колебанием (см. теоретическое введение к лабораторным работам № 9 и 10). Колебания возникают, когда системе, способной совершать колебательные движения (осциллятору), сообщается энергия. В упругих средах колебания, возбужденные в некоторой точке, способны распространяться в них, поскольку упругие среды представляют собой ансамбль связанных между собой частиц. Распространение колебаний частиц упругой среды в пространстве с течением времени называется волновым процессом или волной. Характерным свойством любого волнового процесса является перенос в пространстве энергии, в то время как перенос вещества при распространении волны отсутствует. Направление распространения волны характеризуют с помощью понятия луча. Луч – это линия, касательная к которой в каждой точке совпадает с направлением скорости распространения волны. Геометрическое место точек упругой среды, до которых к некоторому моменту времени распространилось колебательное движение, называется фронтом волны. Геометрическое место точек упругой среды, совершающих колебания в одинаковой фазе, называется волновой поверхностью. Фронт волны и волновые поверхности всегда перпендикулярны направлению распространения волны.

Существует два типа волн: продольные волны, в которых частицы среды колеблются в направлении распространения волны (вдоль луча), и поперечные волны, в которых частицы среды колеблются в направлении, перпендикулярном к направлению распространения волны (перпендикулярно лучу). Продольные волны могут возбуждаться, когда в среде возникают упругие силы при деформации растяжения и сжатия, т. е. в твердых телах, жидкостях и газах. Поперечные волны возбуждаются только в твердых телах, в которых упругие силы могут возникать при деформации сдвига.

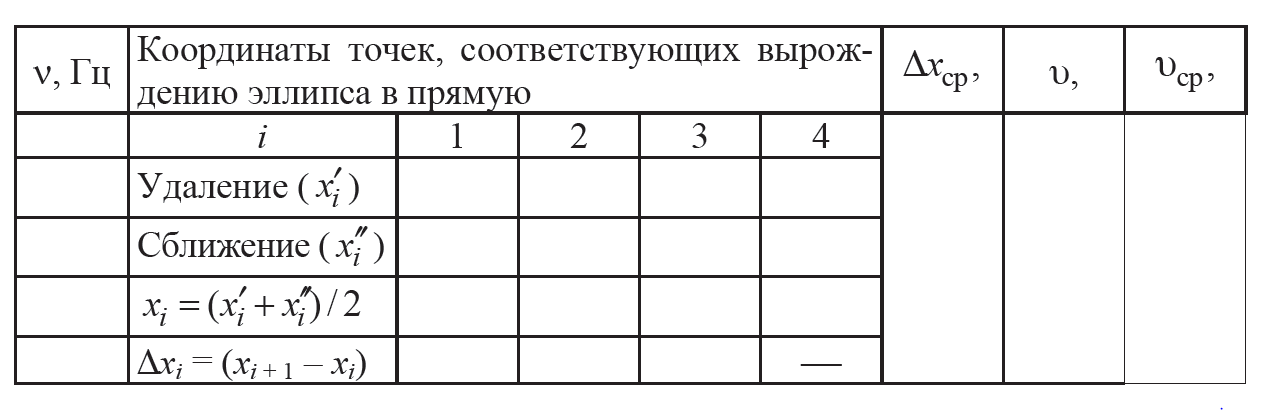
Длиной волны λ называют расстояние, на которое распространяется волна за время, равное периоду колебаний Т:

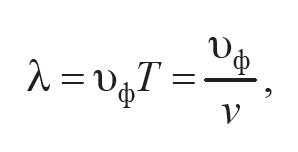
Формула 11.1

где υ_φ – фазовая скорость, показывающая скорость распространения волновой поверхности с определенным значением фазы; ν = 1/ Т – частота колебаний.

В зависимости от размеров источника колебаний и расстояния от источника до точки наблюдения волны можно рассматривать либо как сферические, либо как плоские волны. Сферическая волна формируется точечным источником колебаний и характеризуется волновой поверхностью в виде сферы. Плоская волна формируется протяженным (плоским) источником, а ее волновые поверхности представляют собой параллельные плоскости. Если расстояние от точечного источника колебаний до точки наблюдения велико, то волну можно рассматривать как плоскую.

Для плоской волны, распространяющейся в положительном направлении оси x в непоглощающей упругой среде, смещение от равновесного положения частиц среды на волновом фронте s будет зависеть только от координаты x и времени t, т. е. s = s(x, t). Для точек, лежащих в плоскости x = 0,

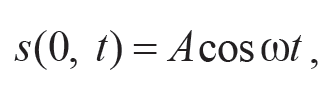
Формула 11.2

где А – амплитуда волны; ω = 2πν – циклическая частота. На расстоянии x от начала координат колебания частиц будут отставать по времени на величину τ = х / υφ – время прохождения волной расстояния x.

Уравнение колебаний частиц, лежащих в плоскости с координатой x, имеет вид

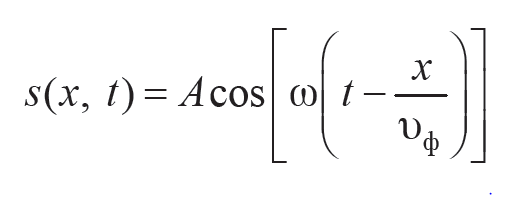
Формула 11.3

и называется уравнением плоской волны. Уравнение плоской волны показывает, что колебания являются периодичными не только во времени, но и в пространстве. Для описания периодичности в пространстве вводят понятие волнового числа:

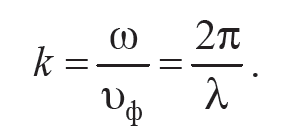
Формула 11.4

Уравнение (11.3) с учетом выражения (11.4) записывается в виде

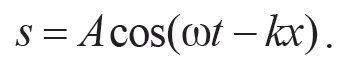
Формула 11.5

Уравнение сферической волны, распространяющейся в изотропной непоглощающей среде, имеет вид

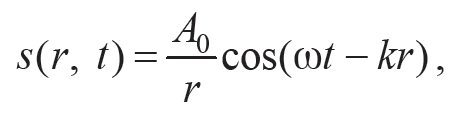
Формула 11.6

где r – расстояние от точечного источника до рассматриваемой точки среды. Характерно, что амплитуда сферической волны A = A₀ / r убывает с расстоянием, поскольку величина энергии волны, приходящаяся на единицу площади волнового фронта, убывает с расстоянием по закону ~1/r². Уравнения плоской (11.5) и сферической (11.6) волн являются решениями волнового уравнения (10.1).

Если некоторая частица одновременно участвует в нескольких колебаниях либо через точку, в которой находится эта частица, распространяется несколько волн, то для определения результирующих характеристик колебательного или волнового процессов применяют методы сложения колебаний. Для сложения колебаний одинакового направления удобно использовать метод векторных диаграмм. В данном методе гармоническое колебание x = Acos(ωt + φ) представляют в виде вектора A, модуль которого равен амплитуде колебаний |A| = A и который направлен под углом φ к оси x. Привращении этого вектора с угловой скоростью, равной циклической частоте колебаний ω , его проекция на ось x будет изменяться по заданному гармоническому закону.

Представим два колебания с одинаковой частотой ω и начальными фазами φ₁ и φ₂ с помощью векторов A₁ и A₂(рис. 11.1). По правилам сложения векторов построим результирующий вектор A = A₁ + A₂. Очевидно, что проекция вектора A на ось x равна сумме проекций х₁ = OE и x₂ = ED слагаемых векторов. Следовательно, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью ω, что и векторы A₁ и A₂, так что результирующее движение будет гармоническим колебанием с частотой ω, амплитудой А и начальной фазой φ:

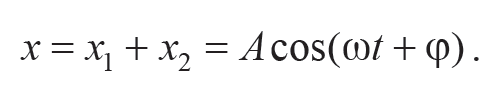
Формула 11.7

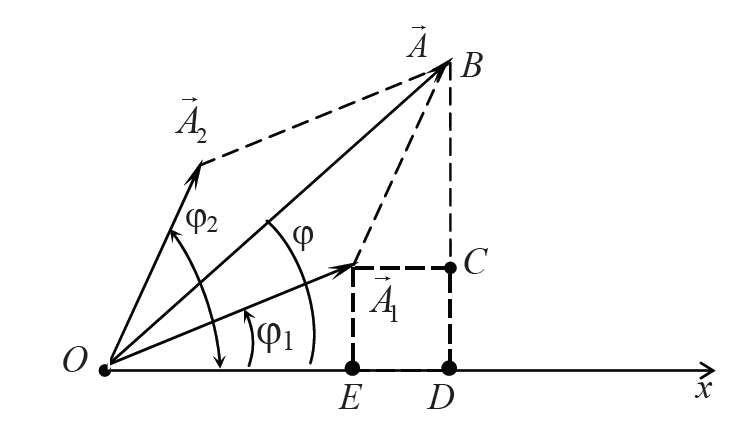
Рисунок 11.1

Из векторной диаграммы (рис. 11.1) видно, что величины А и φ легко определяются из соотношений (11.8) и (11.9):

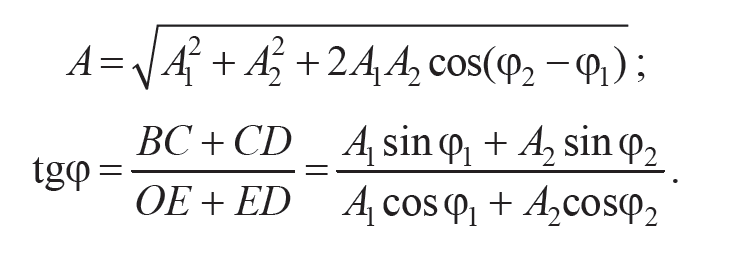
Формулы 11.8, 11.9

Если частоты двух колебаний неодинаковы, то векторы A₁ и A₂ будут вращаться с различной скоростью. Следовательно, в этом случае получим не гармоническое колебание, а более сложный колебательный процесс.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты ω, происходящих во взаимно перпендикулярных направлениях вдоль осей x и y. Выберем начала отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний имеют вид

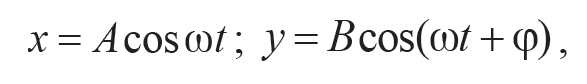
Формула 11.10

где φ – разность фаз этих колебаний. Уравнения (11.10) представляют собой заданное в параметрической форме уравнение траектории, по которой движется точка, участвующая одновременно в двух колебаниях. Чтобы получить уравнение траектории в виде y = ƒ(x), нужно исключить из уравнений параметр время t.

Из первого уравнения получим, что cosωt = x / A, и, используя равенство cos² ωt + sin² ωt = 1, запишем

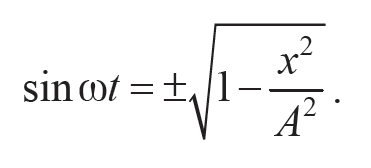
Формула 11.11

Из второго уравнения, используя формулу для косинуса суммы (11.12) и с учетом (11.11), получим

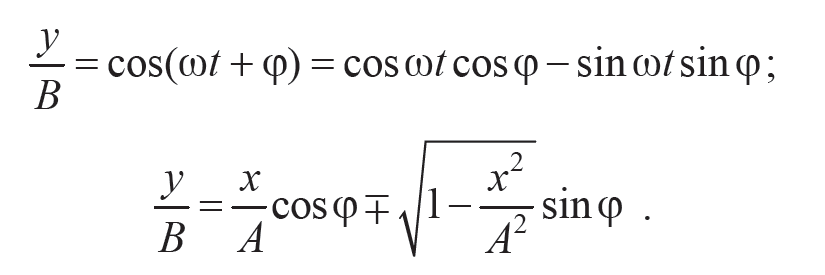
Формулы 11.12 и 11.13

Перенесем первое слагаемое из правой части уравнения в левую и возведем обе части уравнения в квадрат. В результате получим уравнение траектории в общем виде

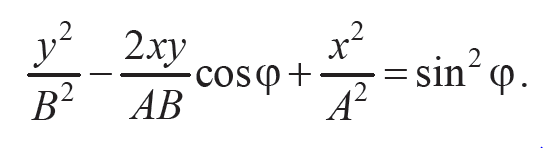
Формулы 11.14

Данное уравнение является уравнением эллипса, оси которого повернуты относительно координатных осей x и y. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний А и В и разности фаз φ. Если разность фаз колебаний φ = 0, ± π, то уравнение эллипса (11.14) преобразуется в уравнение прямой (11.15):

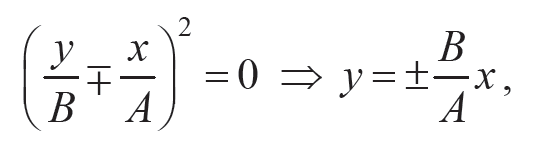
Формулы 11.15

а результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$\sqrt{A_2 + B_2}$$ . Если разность фаз колебаний φ = ±π/ 2, то уравнение (11.14) примет вид

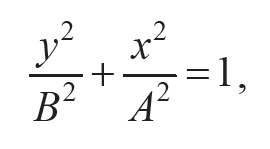
Формулы 11.16

представляющее собой уравнение эллипса, оси которого совпадают с осями координат. При A = B эллипс принимает форму окружности. Отметим, что положительные и отрицательные знаки разности фаз φ отражают движение по и против часовой стрелки, соответственно.

Схема экспериментальной установки для измерения скорости звука в воздухе представлена на рис. 11.2.

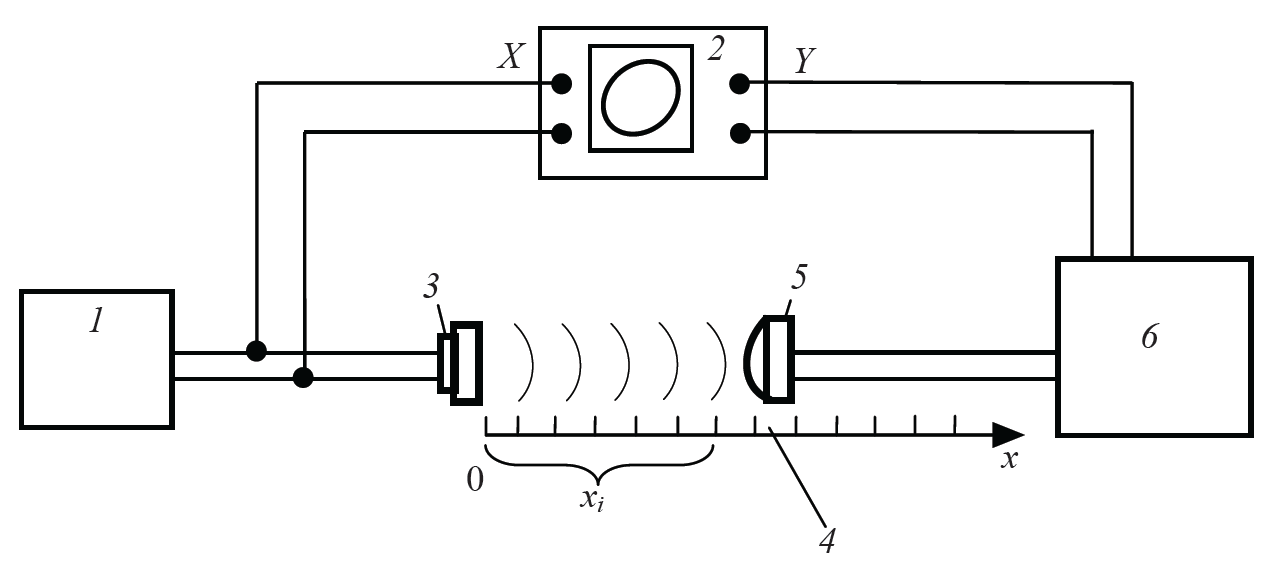
Рисунок 11.2

Звуковой генератор 1 служит для создания в цепи электрических колебаний звуковой частоты. Сигнал с выхода звукового генератора одновременно подается на вход Х осциллографа 2 и на телефон 3. Формируемая на экране осциллографа светящаяся точка под действием сигнала, поданного на вход Х, совершает гармонические колебания в горизонтальном направлении. Электрический сигнал в телефоне преобразуется в звуковую волну, которая распространяется вдоль линейки 4. Микрофон 5 воспринимает звуковую волну и преобразует ее обратно в электрический сигнал, который усиливается усилителем напряжения звуковой частоты 6 и поступает на вход Y осциллографа, где он отклоняет электронный пучок в вертикальном направлении.

Поскольку электрические сигналы распространяются со скоростью света, а скорость распространения звука в воздухе значительно меньше, то колебания светящейся точки на экране осциллографа в вертикальном направлении отстают по фазе от колебаний в горизонтальном направлении на величину 2πm + φ, где m – целое число. Таким образом, светящаяся точка описывает траекторию, которая является результатом сложения двух взаимно перпендикулярных колебаний, сдвинутых относительно друг друга по фазе: х = а cos2πνt, y = bcos(2πνt – φ), где а, b – амплитуды колебаний; ν – частота звукового сигнала, задаваемая генератором. Телефон закреплен неподвижно, а микрофон может перемещаться вдоль линейки, что позволяет изменять разность хода двух волн и, соответственно, сдвиг фаз φ. Таким образом, перемещая микрофон, получаем на экране траектории движения точки различной формы (рис. 11.3). При φ = nπ (n = 0, ±1, ±2, ...) эллипс вырождается в прямую.

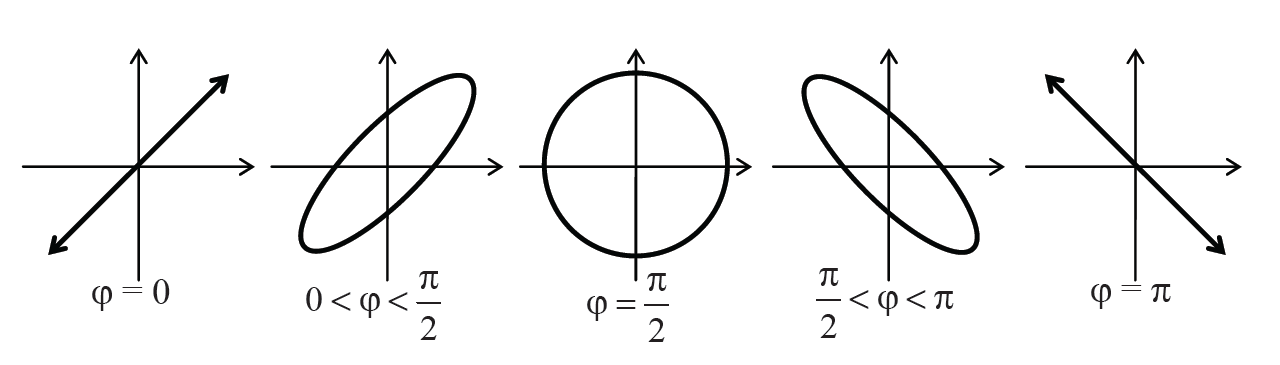
Рисунок 11.3

Таким образом, изменение разности фаз φ, которое соответствует двум соседним положениям (Δn = 1) микрофона, при которых наблюдаются прямые линии, изображенные на рис. 11.3, равно

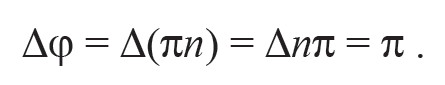
Формула 11.17

Звук в газе представляет собой продольную волну, в которой колебания частиц среды (воздуха) происходят в направлении распространения волны. Колебания воздуха вблизи телефона, расположенного в начале отсчета х = 0, происходят по закону s = Аcos(2πνt), а колебания воздуха вблизи микрофона, удаленного на некоторое расстояние х, запаздывают по фазе на φ:

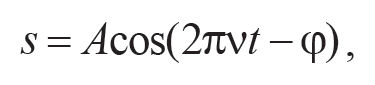
Формула 11.18

где φ = 2πх / λ. Поэтому изменение разности фаз φ и изменение расстояния х связаны соотношением

Формула 11.19

Приравняв выражения (11.17) и (11.19), получим формулу для определения длины волны λ = 2Δх. Тогда скорость звука равна

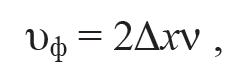
Формула 11.20

где Δх – расстояние между соседними положениями микрофона, для которых эллипс на экране вырождается в прямую.