Момент импульса l_O материальной точки М относительно точки О рассчитывается по формуле, которая аналогична моменту силы F относительно центра О (см. лаб. раб. № 6), т. е.

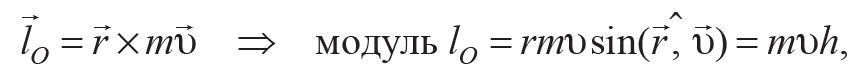
Формула 8.1

где h – плечо импульса p = mυ относительно точки О.

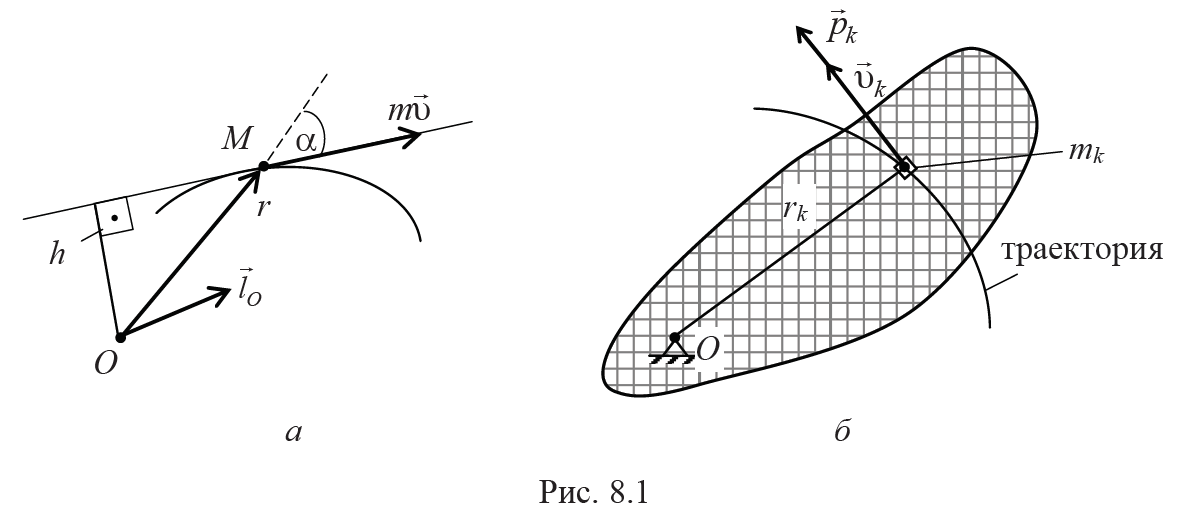
Направление вектора l_O определяется по правилу векторного произведения двух векторов, т. е., например, по правилу правой руки. Для векторов, изображенных на рис. 8.1, а момент импульса l_O направлен перпендикулярно плоскости рисунка «от нас».

Если тело вращается с угловой скоростью ω вокруг неподвижной оси O_z (рис. 8.1, б), которая перпендикулярна рисунку, то все его частицы массами m_k движутся по окружностям с радиусами r_k. Их линейная скорость υ_k = ωr_k, а модуль импульса р_k = m_kυ_k = m_kr_kω.

Модуль момента импульса тела относительно оси Oz равен сумме моментов импульсов всех частиц тела (свойство аддитивности):

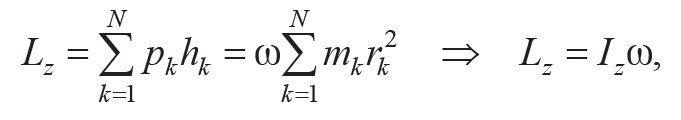
Формула 8.2

где h_k – плечо импульса p_k относительно оси Oz; $$I_z={\sum_{k=1}^N}m_kr^2_k$$ – осевой момент инерции тела (см. лаб. раб. № 6).

Скорость изменения момента импульса L_O механической системы относительно центра О равна сумме моментов всех внешних сил $$\vec{F^e_k}$$, действующих на точки и тела этой системы, т. е.

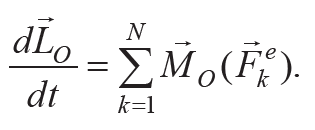
Формула 8.3

Если сумма моментов всех внешних сил равна нулю во время движения, то вектор L_O не изменяется во времени, т. е. L_O = const (закон сохранения момента импульса L_O). В частном случае, если сумма моментов всех внешних сил относительно оси Oz все время равна нулю, то момент импульса системы относительно этой оси не изменяется, т. е. L_z = const (закон сохранения проекции вектора L_O).

Крутильный баллистический маятник (рис. 8.2) выполнен в виде крестовины, подвешенной на проволочном тросе 11 к кронштейну 10. Для устранения маятниковых боковых колебаний к крестовине с помощью троса 11' крепится тяжелый груз 9. Покрытая слоем пластилина мишень 5 укреплена на правом конце горизонтальной штанги, по которой могут перемещаться три цилиндрических груза 5, 6, 7. Меньший из них 6 служит для уравновешивания мишени, а два одинаковых цилиндрических груза 7 и 8 служат для изменения момента инерции маятника. Для определения угла поворота φ маятника используется лазер 12, прикрепленный к оси крестовины. Угол φ определяется по смещению S светового зайчика 13 по круговой шкале радиуса R (на рис. 8.2 она не показана), т. е. φ = S / R.

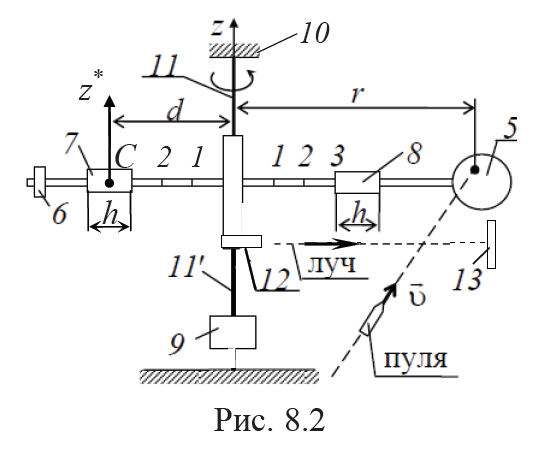
После выстрела пуля массой m, летящая со скоростью υ, попадает в мишень и застревает в ней, создавая в пластилине углубление, на расстоянии r от оси вращения. Рассмотрим движение системы, состоящей из маятника и пули. Моменты всех внешних сил (сил тяжести, сил реакции опор), действующих во время удара на систему, относительно оси вращения z равны нулю (почему это так, разберитесь самостоятельно, изобразив все внешние силы на рис. 8.2). Поэтому применяем закон сохранения проекции момента импульса относительно этой оси (L_1z = L_2z, где L_1z = mυr – момент импульса пули до попадания ее в мишень маятника; L_2z = (I_z + mr²)ω – момент импульса системы после попадания пули), т. е.

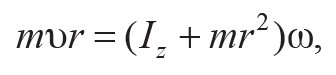
Формула 8.4

где I_z и mr² – моменты инерциии маятника и пули относительно оси вращения соответственно; ω – угловая скорость вращения системы маятник – пуля сразу после соударения.

Начальная кинетическая энергия вращающегося маятника с застрявшей после удара пулей (К_вр = (I_z + mr²)ω² / 2) постепенно превращается в энергию упругой деформации кручения двух одинаковых проволок подвески, так что в момент остановки маятника в крайнем положении потенциальная энергия $$П = 2 f ϕ^2_М / 2$$ (f – модуль кручения проволоки; φ_м – максимальный угол поворота маятника).

В соответствии с законом сохранения энергии (если пренебречь сопротивлением воздуха) получим

Формула 8.5

Исключая из уравнений (8.4) и (8.5) неизвестную угловую скорость ω и учитывая, что φ = S / R, получим расчетную формулу для косвенного измерения скорости υ пули (сделайте это самостоятельно):

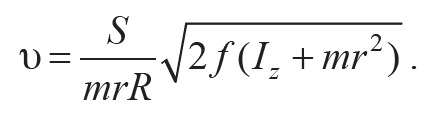
Формула 8.6

Используя свойство аддитивности и теорему Штейнера, находим момент инерции I_z маятника:

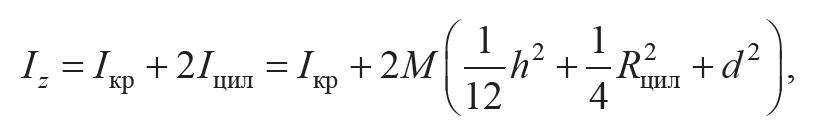
Формула 8.7

где І_кр – момент инерции крестовины с мишенью 5 и противовесом 6; $$I_{цил}=I^{цил}_{Cz^*}+Md^2$$ – момент инерции цилиндрических грузов 7, 8 относительно оси вращения маятника.

Параметры установки. Модуль кручения проволоки f = 4,5 · 10^–2 Н·м. Момент инерции крестовины с мишенью и противовесом І_кр = 0,18 кг·м². Масса М, высота h и радиус R_цил подвижных цилиндров: М = 1,82 кг; h = 8 см; R_цил = 3 см.

Расстояния d от оси вращения маятника до центра тяжести С подвижных цилиндрических грузов при совмещении их ближайших к оси z оснований с метками на горизонтальной штанге крестовины, см: для первой метки d₁ = 8,5; для второй – d₂ = 9,5; для третьей – d₃ = 10,5; для четвертой – d₄ = 11,5 для пятой – d₅ = 12,5; для шестой – d₆= 13,5; для седьмой – d₇ = 14,5; для восьмой – d₈ = 15,5. Массы m пуль указаны на крышке коробки с пулями (номер пули соответствует числу круговых меток, нанесенных на поверхности этой пули).