



Для материальной точки массой m, движущейся со скоростью υ, кинетическая энергия K=mυ2/2, поэтому кинетическая энергия системы из N материальных точек с учетом ее аддитивности рассчитывается по формуле

Формула 7.1
При поступательном движении тела массой m все его частицы массой mk, на которые мысленно можно разбить тело, имеют одинаковые скорости, равные скорости центра масс (υk=υC). Следовательно
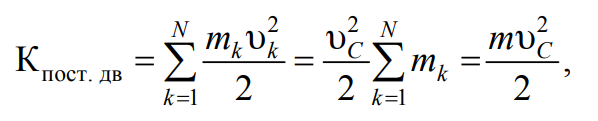
Формула 7.2
где m=∑mk – масса тела.
При вращательном движении тела все его частицы массой mk движутся по окружностям радиуса rk (рис. 6.4). Скорости этих частиц рассчитываются по формуле υk=ωrk (ω – угловая скорость тела (см. лаб. раб. № 6)). В результате из формулы (7.1) следует, что
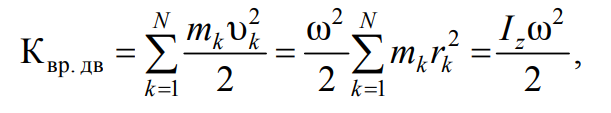
Формула 7.3
где Iz=∑mkrk2 – момент инерции тела относительно оси z.
Для консервативных сил, работа которых не зависит от формы траектории движущейся материальной точки, можно ввести понятие потенциальной энергии этой точки в силовом поле. Эта энергия по определению равна работе А консервативной силы, которая выполняется при переходе материальной точки из произвольной точки Р с координатами x, y, z на нулевой уровень О, где потенциальная энергия П полагается равной нулю, т. е.
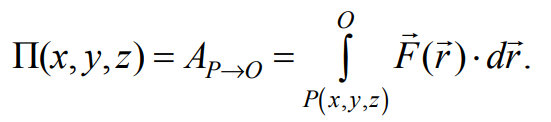
Формула 7.4
Примеры вычисления потенциальной энергии.
Потенциальная энергия материальной точки массой m в поле сил тяжести.
На точку массой m на высоте h = z со стороны поля действует сила тяжести FT=mg (рис. 7.1). Скалярное произведение для элементарной работы δA=Fdrв формуле (7.4) запишем в координатной форме:
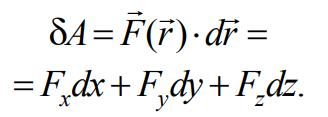
Формула 7.5
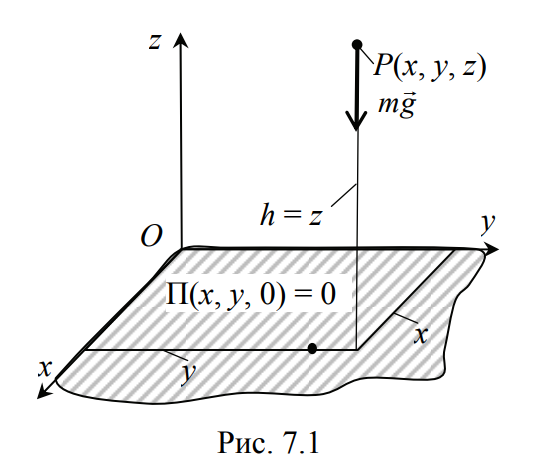
В этом примере проекции Fx и Fy для силы FT равны нулю, а Fz=-mg. Нулевой уровень О для потенциальной энергии выберем при z = 0, т. е. на горизонтальной плоскости xy. В результате с помощью (7.4) получим
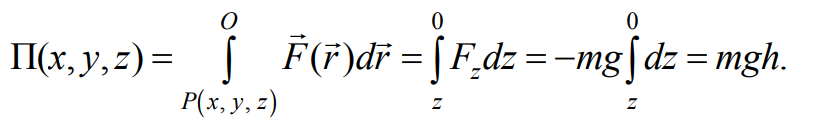
Формула 7.6
Потенциальная энергия сил упругости.
В соответствии с законом Гука сила упругости Fупр деформированной пружины пропорциональна ее абсолютной деформации x=Δl=l-l0 (рис. 7.2), l0– длина недеформированной пружины, тогда ее проекция
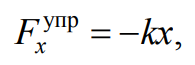
Формула 7.7
где k – коэффициент жесткости пружины.
Из определения (7.4) найдем
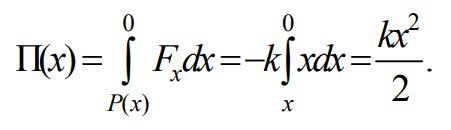
Формула 7.8
Здесь нулевой уровень выбран в положении, которое соответствует недеформированной пружине длиной l0, т. е. в точке О.
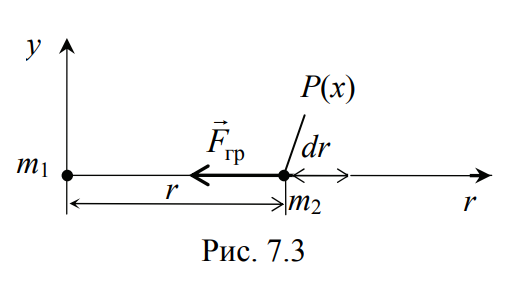
Потенциальная энергия гравитационного поля.

Сила всемирного тяготения (гравитации) определяется по формуле Fгр=γm1m2/r2, γ – гравитационная постоянная; r – расстояние между точечными массами m1 и m2.
Выполняя расчеты, будем считать, что точка массой m1 неподвижна, а точка массой m2 движется (рис. 7.3). Далее учтем, что, поскольку работа консервативных сил не зависит от формы траектории, то наиболее удобно провести интегрирование вдоль радиального направления (т. е. оси r), выбрав нулевой уровень на бес-конечности (П(∞) = 0). В результате получим
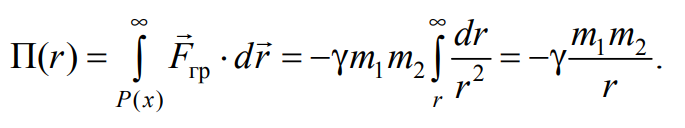
Формула 7.9
Если на систему материальных точек и (или) тел действуют диссипативные силы, то для этой системы механическая энергия Е = К + П будет изменяться. Изменение механической энергии определяется работой Aдис диссипативных сил:

Формула 7.10
Работа диссипативных сил, т. е. сил трения и сопротивления, отрицательна, поэтому энергия Е уменьшается, превращаясь в тепловую энергию, которая рассеивается в окружающей среде, т. е. имеет место диссипация энергии.
Если на систему действуют только консервативные силы (внешние и внутренние), т. е. Aдис=0, из (7.10) следует, что механическая энергия сохраняется (Е = К + П = const). Это утверждение называют законом сохранения механической энергии.
Маятник Максвелла (рис. 7.4, а) представляет собой массивный диск 1 на оси 2, подвешенной на двух нитях 3, которые закреплены на неподвижном верхнем кронштейне 4 (бифилярная подвеска). При вращении диска 1 нити наматываются (или разматываются) на ось, которая при этом движется поступательно в вертикальном направлении. Подвижный кронштейн 5 можно перемещать вдоль вертикальной стойки, на которую нанесена миллиметровая шкала для установления заданного расстояния h1 между кронштейнами. В кронштейнах 4 и 5 находятся фотоэлек-трические датчики. Ворот 6 используется для закрепления и регулирования длины бифилярной подвески маятника, а элек-тромагнит 7 – для удержания маятника в верхнем положении.
Для изменения момента инерции маятника на диск 1 накладываются кольца разной массы. Время падения измеряется с помощью секундомера 8.
Если поднять маятник в верхнее положение и отпустить его, то под действием силы тяжести ось Cx маятника начнет опускаться (рис. 7.4, б). Пренебрегая силами сопротивления воздуха и неупругой деформацией нитей, можно воспользоваться формулами равноускоренного движения и получить расчетную формулу для косвенного измерения скорости оси, т. е. центра масс С маятника в его нижнем положении (после опускания на высоту h1):
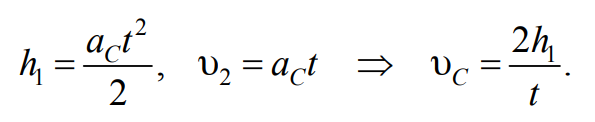
Формула 7.11
С другой стороны, пренебрегая диссипативными силами (со-про¬тивлением воздуха и неупругой деформацией нитей), можно использовать закон сохранения механической энергии. В верхнем положении маятник массой т обладает потенциальной энергией П = mgh. Перемещаясь на расстояние h в нижнее положение, потенциальная энергия маятника переходит в кинетическую энергию поступательного и вращательного движений. Приравнивая механическую энергию в верхнем и нижнем положениях маятника, получим
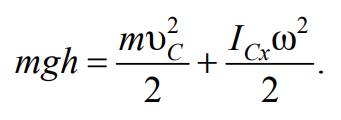
Формула 7.12
Угловая скорость ω диска маятника связана со скоростью его поступательного движения, т. е. со скоростью υC его центра масс ( ω=υC/Ro, где Ro – радиус оси). После подстановки ω=υC/Ro в формулу (7.12) получаем теоретическую формулу для скорости центра масс маятника:
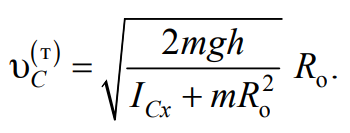
Формула 7.13
Используя свойство аддитивности, находим массу и осевой момент инерции маятника по следующим формулам:
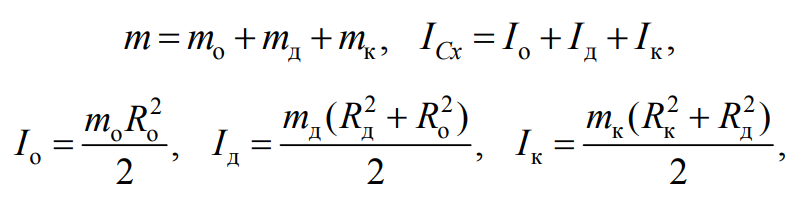
Формула 7.14
mo, mд, mк и Ro, Rд, Rк – соответственно массы и внешние радиусы оси, диска и кольца.
Полностью избавиться от действия неконсервативных сил со¬противления и неупругой деформации нитей в любой реальной меха¬нической системе практически невозможно. Действие этих сил приводит к частичной потере механической энергии и пре-вращению ее в теплоту (диссипация, т. е. рассеяние энергии в ок-ружающей среде). Потери механической энергии маятника можно оценить, наблюдая за его дальнейшим движением после достижения нижнего положения. Диск, вращаясь по инерции в прежнем направлении, приводит к наматыванию нити в направлении, противоположном начальному. В результате происходит подъем маятника. В идеальном случае (при отсутствии диссипации) максимальная высота h2 подъема была бы в точности равна первоначальной высоте h1. Практически на опыте маятник поднимается на меньшую высоту h2=h1-Δh12. Таким образом, потеря механической энергии за время опускания и подъема равна mgΔh12, а за время опускания она равна половине этой потери, т. е. mgΔh12/2. Поэтому, если в формуле (7.13) используем значение h=h1, то получаем завышенное значение теоретической скорости υC(т) по сравнению с ее истинным значением. Для учета этой систематической погрешности нужно в левой части уравнения (7.12) использовать только ту часть потенциальной энергии, которая фактически превращается в кинетическую энергию маятника, поэтому надо положить
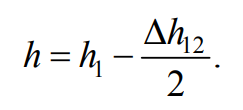
Формула 7.15
Совпадение значений скорости υC, рассчитанных по формулам (7.11) и (7.13) с учетом (7.15), будет свидетельствовать о выполнении закона сохранения механической энергии, который был использован при выводе формулы (7.13).
1. Подготовьте таблицу для занесения и обработки результатов измерений.
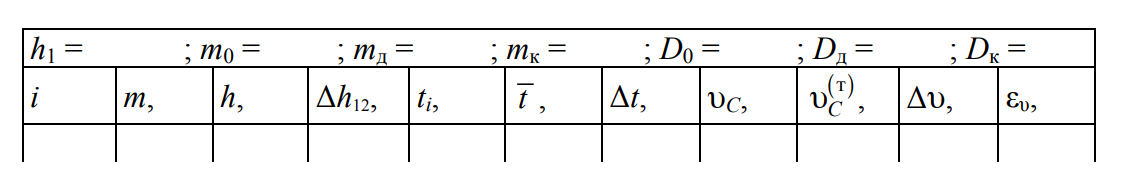
2. В комплекте к установке возьмите кольцо, номер которого совпадает с номером группы в потоке. Если номер звена в под-группе четный, то h1=38 см, если нечетный – h1=41 см.
3. Установите подвижный кронштейн 5 так, чтобы его указатель высоты совпал с заданным значением h1. Наложите кольцо на диск, прижимая до упора. Массы оси, диска и кольца и их диаметры, указанные на этих деталях маятника, занесите в таблицу.
4. Придерживая ворот 6, отпустите его стопорную гайку. Вращая ворот, установите длину нитей подвески, при которой нижний край кольца маятника будет примерно на 3 мм ниже оптической оси нижнего фотоэлектрического датчика (на уровне оптической оси датчика на кронштейне нанесена горизонтальная линия). Одновременно произведите корректировку подвески маятника, обращая внимание на то, чтобы его ось была параллельной основанию прибора. Блокируйте ворот, зажав гайку. Включите вилку шнура в розетку и нажмите кнопку «СЕТЬ». Утопите кнопку «ПУСК».
5. Вращая маятник, намотайте на вал нити подвески. Следите, чтобы она наматывалась равномерно, виток к витку. Отпустите кнопку «ПУСК» и зафиксируйте маятник с помощью электромагнита в верхнем положении. Если при удерживании электромагнитом маятника нити подвески слишком натянуты, поверните диск маятника так, чтобы точки на ободе кольца сместились на 2–3 мм в обратном направлении по отношению к наматыванию нити.
6. Нажмите кнопку «СБРОС», затем утопите кнопку «ПУСК». Как только маятник начнет падать, откроется световой поток, падающий на верхний фотодатчик. В результате включится секундомер, который выключится, как только маятник перекроет световой поток, падающий на нижний фотодатчик. Тем самым будет измерено время t падения маятника. Продолжайте следить за маятником во время подъема и задержите его на максимальной высоте. Измерьте расстояние Δh12 между верхним краем кольца и линией на корпусе электромагнита. Значения t и Δh12 занесите в таблицу.
7. Пункты 5, 6 опыта повторите еще 5 раз (i = 2, ..., 6). Выключите установку.
8. Найдите среднее значение $$\overline{t}$$ и по формуле (7.11) рассчитайте среднее значение скорости $$\overline{υ_C{^{(т)}}}$$
9. По формуле (7.13) с учетом (7.14), (7.15) вычислите теоре-тическое значение скорости υC(т).
10. Согласно методике прямых измерений определите абсо-лютные погрешности Δh1 и Δt ( Δh1 рассматривайте как приборную погрешность, a Δt – как случайную). Самостоятельно выведите формулу для относительной погрешности ευ косвенного измерения скорости, которая имеет следующий вид:
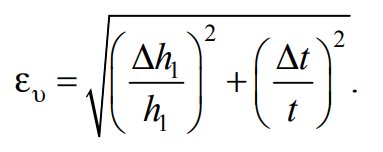
Вычислите ευ, а также абсолютную погрешность Δυ=ευυC.
11. Подготовьте выводы по выполненной лабораторной работе.