



Все твердые тела под действием внешних сил изменяют свои размеры и форму, т. е. деформируются. Если после прекращения действия сил тело принимает первоначальные размеры и формы, то деформация называется упругой. Если деформации сохраняются после снятия нагрузки, то их называют пластическими (или остаточными). Деформация является упругой при условии, что она невелика и длится недолго. Упругие деформации используются всюду, начиная от различного типа амортизационных устройств (рессор, пружин и т. д.) и кончая тончайшими измерительными приборами. На пластической деформации основаны различные способы обработки металлов (штамповка, ковка, прокатка и т. д.).
Под действием внешних сил при деформации происходит смещение частиц (атомов), составляющих тело, из их равновесных положений. Возникающие при этом силы взаимодействия этих частиц препятствуют деформации тела. Эти внутренние силы называют силами упругости Fупр. Они уравновешивают внешние силы F, приложенные к телу: Fупр=-F. Величина, равная отношению силы к площади поверхности, на которую действует сила, называется напряжением:
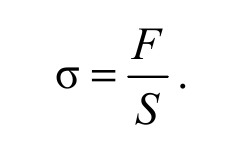
Формула 2.1
Благодаря взаимодействию частей тела друг с другом напряжение передается во все точки тела – весь объем тела оказывается в напряженном состоянии. Если сила направлена по нормали к поверхности, напряжение называют нормальным σn, если же по касательной к поверхности – тангенциальным (касательным) στ.
К простейшим видам деформации относятся деформации растяжения (или сжатия) и сдвига. Они принадлежат к однородным деформациям, при которых все элементы тела деформируются одинаково. Выделяют также деформации изгиба и кручения, которые сводятся к комбинациям простейших деформаций.
Деформации растяжения (сжатия) (рис. 2.1, а) стержня характеризуются абсолютным удлинением Δl = l – l0, где l – длина деформированного стержня и l0 – длина недеформированного стержня. При упругих деформациях справедлив закон Гука, согласно которому деформирующая сила и величина деформации пропорциональны друг другу:
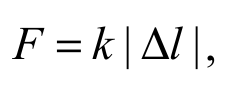
Формула 2.2
где коэффициент k называют жесткостью стержня.
Заметим, что изменение длины стержня сопровождается изменением его поперечных размеров. Из опыта следует, что изменение диаметра стержня Δd связано с изменением его длины Δl соотношением
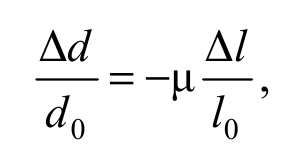
Формула 2.3
где d0 – первоначальный диаметр стержня; μ – коэффициент Пуассона, зависящий от свойств материала. Обычно при растяжении (сжатии) продольные размеры тел уменьшаются (увеличиваются). Для таких тел 0 < μ < 0,5. Существуют также материалы, у которых коэффициент Пуассона отрицателен. Это значит, что при растяжении поперечные размеры таких тел увеличиваются и наоборот. Такие материалы называют ауксетиками.
Деформацией сдвига называют такую деформацию твердого тела, при которой плоские слои тела, параллельные некоторой плоскости, смещаются друг относительно друга под действием силы, приложенной по касательной к образцу (рис. 2.1, б). При упругих деформациях выполняется закон Гука для сдвига:

Формула 2.4
где kсд – коэффициент жесткости при сдвиге, зависящий от упругих свойств твердого тела и его размеров; Δа – абсолютный сдвиг между слоями, которые расположены на расстояние b друг от друга.
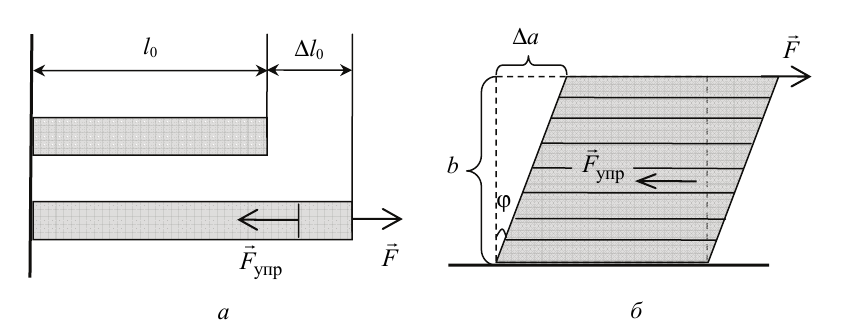
Рисунок 2.1
Из опыта следует, что коэффициенты жесткости при растяжении (сжатии) и сдвиге определяются соотношениями
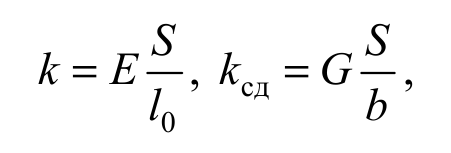
Формула 2.5
где E – модуль Юнга; G – модуль сдвига. Они характеризуют упругие свойства материала, из которого изготовлено тело.
Подставляя (2.5) в (2.2) и (2.4) и принимая во внимание (2.1), получим законы Гука для относительной деформации при растяжении (сжатии) и сдвиге
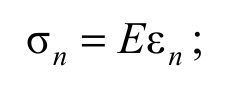
Формула 2.6
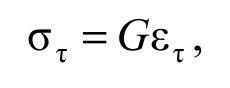
Формула 2.7
где εn и ετ относительные деформации при растяжении (сжатии) и сдвиге. Они определяются соотношениями
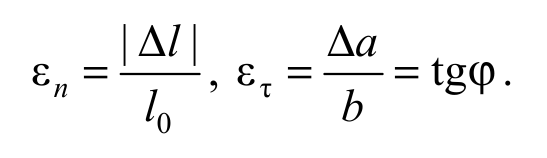
Формула 2.8
где φ – угол сдвига. При упругих деформациях угол φ мал, поэтому tgϕ ≈ φ и ετ ≈ φ.
Из формул (2.6), (2.7) следует физический смысл модулей Юнга и сдвига. Модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение было бы равно F единице (т. е. при изменении длины стержня в два раза), если считать, что при таких напряжениях деформация остается упругой. Модуль сдвига равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45° (γ = tgϕ =1), если бы деформации оставались упругими. В СИ модуль Юнга и сдвига измеряют в паскалях: [E] = [G] = H/м2 = Па.
Изгибом называют деформацию (рис. 2.2, а), при которой нарушается прямолинейность оси прямого бруса. Эта деформация неоднородная, так как разные части бруса деформированы в разной степени. Элементы, расположенные вдоль оси, практически не деформированы, выше оси испытывают деформацию сжатия, а ниже – растяжения.
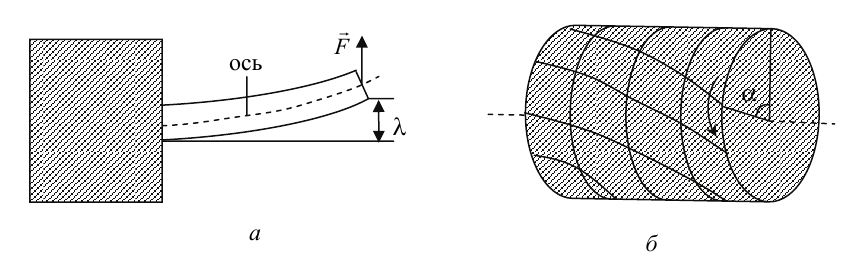
Рисунок 2.2
Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и др. При упругих деформациях справедлив закон Гука при изгибе:
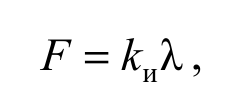
Формула 2.9
где F – изгибающая сила; kи – жесткость бруса при изгибе; λ – стрела прогиба (максимальное смещение оси бруса)
Коэффициент пропорциональности kи зависит от модуля Юнга материала бруса, а также от его размеров и формы поперечного сечения. Например, для бруса прямоугольного сечения справедливо соотношение
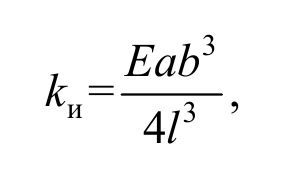
Формула 2.10
где a – ширина бруса; b – толщина бруса; l – длина сгибаемой части бруса.
Кручением называют деформацию твердого тела, при которой под действием внешней силы происходит относительный поворот параллельных сечений тела вокруг некоторой оси (рис. 2.2, б). Мерой абсолютной деформации кручения является угол закручивания α, он неодинаков в различных поперечных сечениях. При закручивании сечения тела испытывают сдвиг относительно друг друга. Эта деформация является неоднородной, так как величина сдвига зависит от расстояния r от оси.
Закон Гука для кручения устанавливает связь между моментом силы M, закручивающего одно сечение относительно другого на угол α:
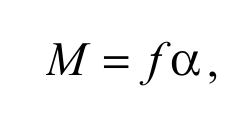
Формула 2.11
где f – модуль кручения. Он зависит от физических свойств тела, его формы и геометрических размеров. Для сплошной проволоки радиусом R и длиной L
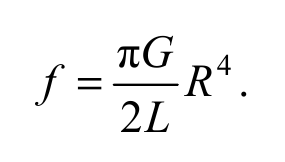
Формула 2.12
Деформацию кручения испытывают валы всех машин, винты, отвертки и т. п., ее часто используют в физических опытах и в измерительных приборах.
Измеряя жесткость kи прямоугольного бруска при изгибе, модуль Юнга материала, из которого изготовлен брусок, можно определить из формулы (2.10):
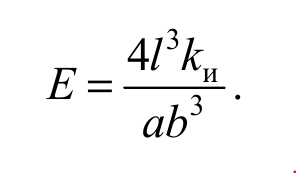
Формула 2.13
На рис. 2.3, а изображена схема установки для измерения жесткости kи бруска, изготовленного из различных пород древесины. Она представляет собой закрепленные на основании опоры А и В. Сквозь них пропущена металлическая труба 1, на середине которой установлены индикатор часового типа 2 для измерения стрелы прогиба λ и чашка 3 для грузов, оказывающих давление на исследуемый брусок 4. Брусок прямоугольного сечения кладется на опоры А и В между индикатором и чашкой для грузов.
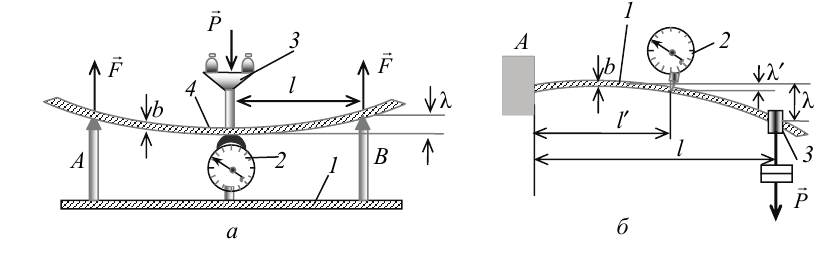
Рисунок 2.3
Под действием силы давления со стороны груза брусок изогнется. Учитывая условие равновесия бруска, изгибающая сила равна половине силы тяжести P, действующей на груз:
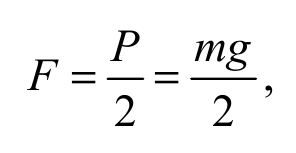
Формула 2.14
где m, – масса грузов, помещенных на чашку 3. Длина изгибаемой части l, равна половине расстояния L, между опорами: l = L / 2,.
Жесткость бруска при изгибе определим из соотношения (2.9):
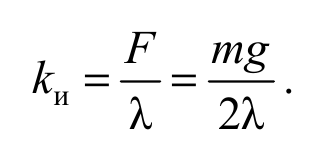
Формула 2.15
На рис. 2.3, б изображена схема установки для измерения жесткости kи бруска, изготовленного из стали. Стальной брусок 1 одним концом закреплен в неподвижной опоре A. Индикатор 2 установлен на расстоянии l′ от опоры, а подвеска 3 с грузами, вызывающими изгиб, – на расстоянии l, которое может изменяться.
Стрела прогиба λ связана с измеряемым прогибом λ′ соотношением
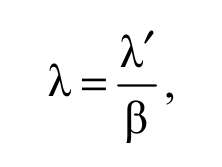
Формула 2.16
где β определяется по формуле
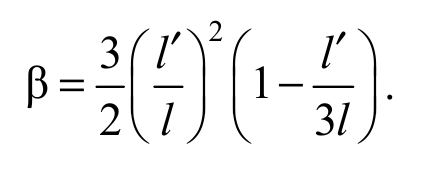
Формула 2.17
Учитывая, что изгибающая сила в этом случае равна силе тяжести груза F = P = mg, из (2.9) найдем жесткость стального бруска:
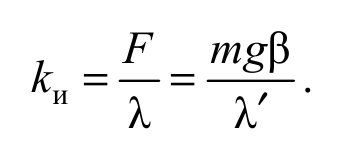
Формула 2.18
Выражения для расчета относительной εE и абсолютной ΔE погрешностей косвенного измерения модуля Юнга по формуле (2.13) следуют из (О10):
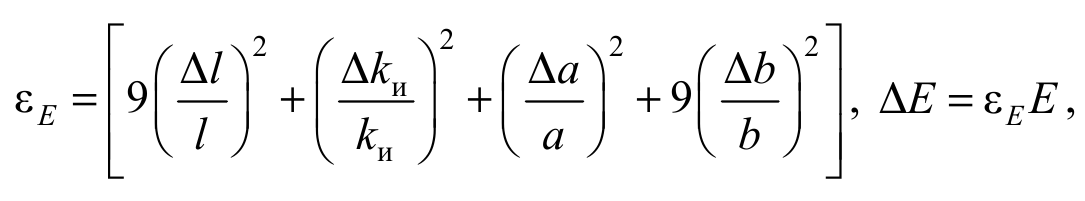
Формула 2.19
где Δl, Δkи, Δa, Δb погрешности соответствующих величин.


