Силы трения возникают при соприкосновении поверхностей тел и препятствуют их относительному перемещению. Различают трение двух видов: внешнее (сухое) и внутреннее (вязкое). Внешним трением называют трение между поверхностями двух твердых тел при отсутствии какой-либо прослойки, например смазки, между ними. Внутренним трением называют трение между твердым телом и жидкой или газообразной средой, а также между слоями такой среды.

Различают три вида внешнего трения: трение покоя, скольжения и качения.

Сила трения покоя возникает при попытке внешней силы F вызвать скольжение одного тела по другому. При значениях внешней силы 0 < F < F₀ тело остается в покое. Сила трения покоя по модулю равна силе, пытающейся сдвинуть тело, и направлена в противоположную сторону (рис. 3.1). Максимальная сила трения покоя пропорциональна силе нормального давления F_n, которая по модулю равна силе реакции опоры F_n = N, т. е.

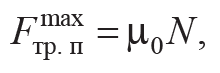
Формула 3.1

где μ₀ – коэффициент трения покоя, он зависит от природы и состояния трущихся поверхностей.

Если внешняя сила F превзойдет по модулю F₀, тело начинает скользить по поверхности, возникает сила трения скольжения, которая также пропорциональна силе нормального давления:

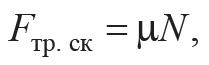
Формула 3.2

где μ – коэффициент трения скольжения, он зависит от природы и состояния трущихся поверхностей, а также от скорости относительного движения тел. Обычно сила трения скольжения с увеличением скорости вначале несколько убывает, а затем начинает расти.

Остановимся на причинах, вызывающих силы трения. Под микроскопом поверхность тела испещрена микроскопическими неровностями. Можно подумать, что трение обусловлено зацеплением выпуклостей друг за друга, но тогда бы сила трения должна была увеличиваться при увеличении площади поверхности соприкосновения тел. Однако опыт показывает, что этого не наблюдается. В действительности трение обусловлено не зацеплением выпуклостей друг за друга, а взаимодействием в точках соприкосновения на молекулярном уровне. Подтверждением этого служит факт, что между очень гладкими поверхностями существует большое трение скольжения. Например, используемые в машиностроении стальные измерительные калибры с тщательно отполированными торцами (плитки Иогансона) благодаря межмолекулярному взаимодействию настолько сильно слипаются, что для их разделения приходится прилагать значительные усилия. Молекулярная модель трения объясняет, почему сила трения не зависит от площади соприкосновения тел. При соприкосновении тел только незначительный процент площади соприкосновения находится в контакте на молекулярном уровне. Тела практически соприкасаются выпуклостями на своих неровных поверхностях. Фактическая площадь соприкосновения не зависит от взаимного расположения тел, а определяется силой, прижимающей тела друг к другу. Молекулярная модель позволяет понять зависимость силы трения от скорости. Когда одно тело начинает перемещаться по поверхности другого, первоначальные связи между молекулами оказываются разорванными и сила трения уменьшается. При увеличении скорости микроскопические выступы начинают разрушаться, и фактическая площадь соприкосновения увеличивается, сила трения скольжения также увеличивается.

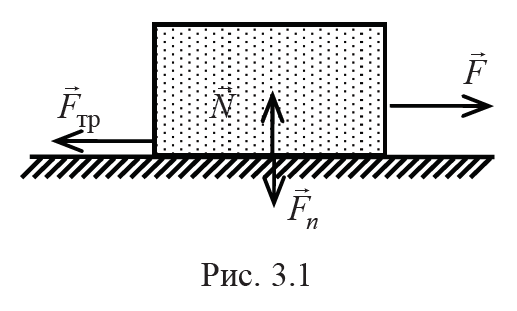
Трение качения возникает при качении одного твердого тела (цилиндра или шара) по поверхности другого. Причиной возникновения трения качения являются деформации самого тела и поверхности, по которой оно катится. При качении абсолютно недеформируемого тела по абсолютно недеформируемой поверхности (рис. 3.2, а) сила реакции N опоры приложена в точке А и лежит на одной линии с силой тяжести P, уравновешивая ее. В этом случае никаких сил сопротивления качению не возникает, оно должно начинаться под действием любой сколь угодно малой силы F.

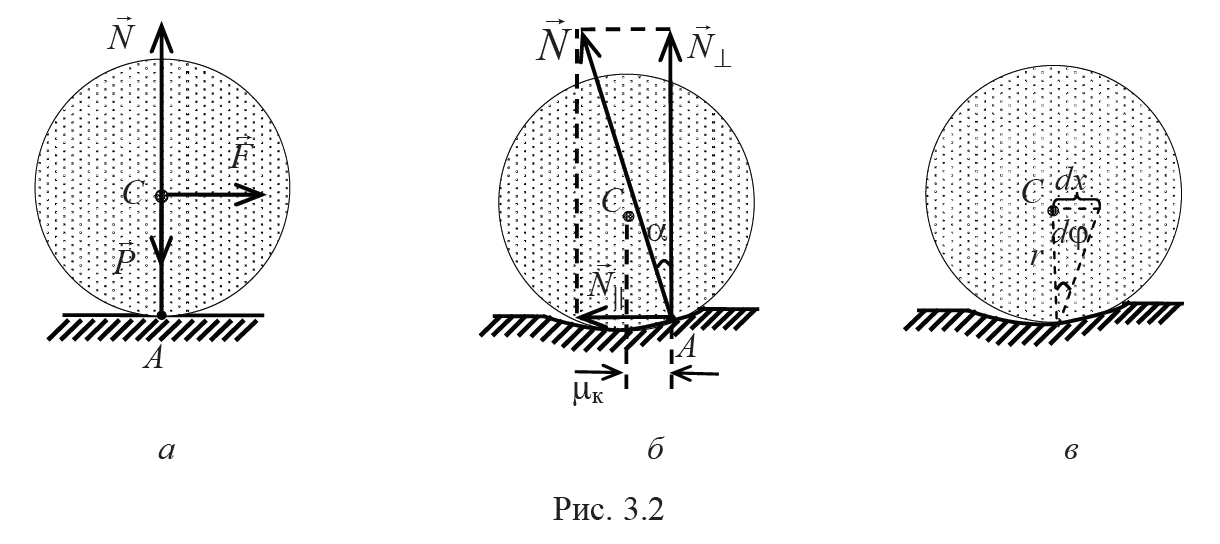
В реальности в точках соприкосновения тела и поверхности возникают деформации. Вследствие этого катящееся тело все время как бы вкатывается на горку (рис. 3.2, б). При этом точка А приложения равнодействующей сил реакции поверхности несколько смещается вперед на расстояние μ_к, а линия действия этой силы отклоняется от вертикали назад. В результате возникает момент силы реакции, замедляющий вращение тела и появляется горизонтальная составляющая N_||, замедляющая поступательное движение тела.

Момент силы реакции относительно оси, проходящей через центр масс тела, имеет вид

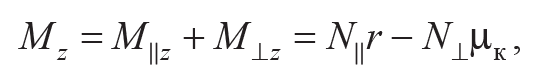
Формула 3.3

где M_||z = N_||r и M_⊥z = –N_⊥μ_к – моменты горизонтальной и вертикальной составляющих сил реакции; r – радиус катящегося тела. При записи (3.3) учтено, что при малых деформациях плечо горизонтальной составляющей N_|| примерно равно радиусу тела.

Заметим, что момент M_||z горизонтальной составляющей силы реакции способствует вращению тела, а замедляет вращение именно момент M_⊥z. Поэтому момент M_⊥z принято называть моментом трения качения. Учитывая, что угол отклонения α мал, вертикальная составляющая силы реакции N_⊥ = Ncosα ≈ N, модуль момента трения качения определяется соотношением

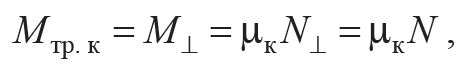
Формула 3.4

где плечо μ_к силы N_⊥ называют коэффициентом трения качения. Заметим, что коэффициент трения качения, в отличие от коэффициента трения скольжения, имеет размерность длины.

Горизонтальную составляющую N_||, противодействующую поступательному движению тела при качении, называют силой трения качения:

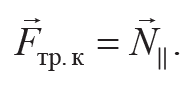
Формула 3.5

Оценить силу трения качения можно по горизонтальной внешней силе F приложенной к оси цилиндра и вызывающей равномерное качение тела по горизонтальной плоскости. В этом случае сила трения качения F_тр.к компенсируется силой тяги F. Угловое ускорение тела, а следовательно и момент силы реакции M_z (3.3), должны быть равны нулю. Линия действия силы реакции опоры N при этом проходит через ось тела. Приравнивая (3.3) к нулю и принимая во внимание (3.4), найдем соотношение для силы трения качения (3.5):

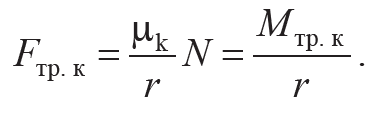
Формула 3.6

В отсутствие силы тяги при качении по горизонтальной поверхности ускорение центра масс тела определяется только горизонтальной составляющей N_|| силы реакции опоры, т. е. силой трения качения. Под действием силы трения качения кинетическая энергия поступательного движения тела уменьшается и ее изменение равно работе силы трения качения. При перемещении центра масс тела на бесконечно малую величину dx работа силы трения качения

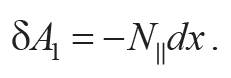
Формула 3.7

При этом изменение кинетической энергии, связанной с вращением тела относительно оси, проходящей через центр масс тела, определяется работой δA₂ момента (3.3) силы реакции:

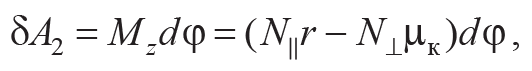
Формула 3.8

где dϕ – угол поворота тела при перемещении его центра масс на dx.

При качении тела без проскальзывания угол поворота dϕ и перемещение dx связаны соотношением dx = rdϕ (рис. 3.2, в). Учитывая это, полное изменение кинетической энергии катящегося тела равно работе:

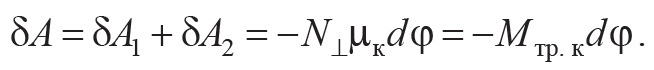
Формула 3.9

Таким образом, изменение полной кинетической энергии тела определяется только моментом трения качения. Отсюда следует, что работа силы реакции при повороте тела на конечный угол  определяется соотношением

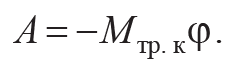
Формула 3.10

Силы внутреннего (вязкого) трения зависят от скорости движения тела в среде. При небольших скоростях движения сила линейно возрастает с увеличением скорости и направлена в противоположную сторону движения:

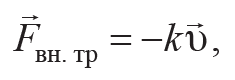
Формула 3.11

где коэффициент k зависит от формы и размеров тела, состояния его поверхности, а также от свойства среды, называемого вязкостью.

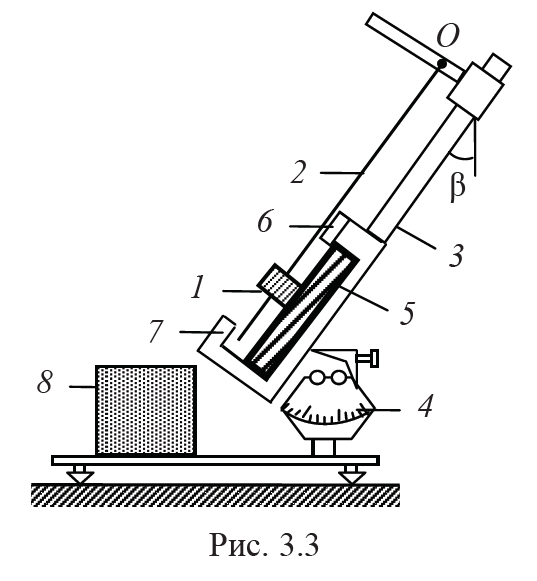
Наклонный маятник (рис. 3.3) состоит из диска 1 (или шарика), который навинчивается на наконечник, подвешенный с помощью нити 2 в точке О на перекладине колонки 3. Колонка может поворачиваться вокруг горизонтальной оси, отклоняясь от вертикали на угол β, который измеряется по шкале 4. Диск опирается на пластину 5, которая устанавливается в пазы кронштейна колонки. Диск и пластина образуют исследуемую пару трения качения и могут быть сделаны из одинаковых или разных материалов. Угол отклонения диска от положения равновесия определяется по шкале 6. Подсчет числа п колебаний диска осуществляет электронная система, основными деталями которой являются фотоэлектрический датчик 7, который соединен с цифровым счетчиком числа колебаний 8.

Если отклонить диск на некоторый угол α от положения равновесия (рис. 3.4, а), а затем отпустить его, он будет совершать затухающие колебания. Уменьшение амплитуды колебаний обусловлено трением качения и сопротивлением воздуха. Силу сопротивления воздуха ввиду ее малости можно не учитывать.

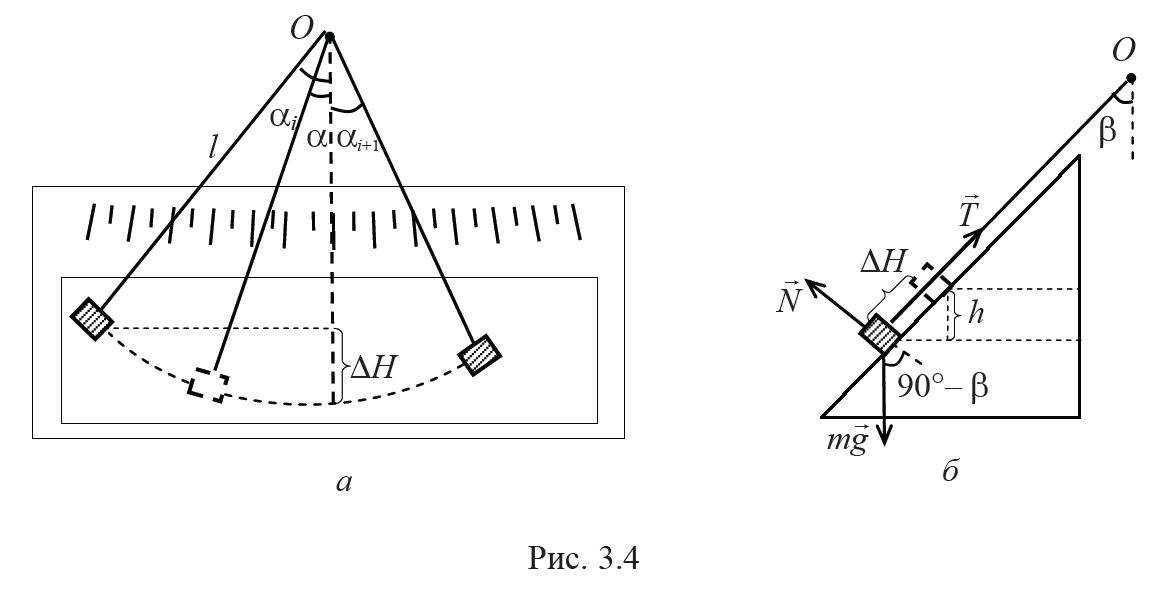
Найдем изменение механической энергии ΔE диска для двух последовательных положений, соответствующих амплитудным (максимальным) отклонениям α_i и α_{i + 1} (рис. 3.4, а).

Так как кинетическая энергия диска в этих положениях равна нулю, то изменение механической энергии равно изменению потенциальной энергии ΔП и определяется работой силы реакции при качении:

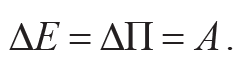
Формула 3.12

При отклонении от положения равновесия на угол α диск поднимется над нулевым уровнем отсчета потенциальной энергии на высоту h = ΔHcosβ (рис. 3.4, б), где ΔH = l – l cosα = 2l sin²(α / 2), l – длина нити (рис. 3.4, а). Его потенциальная энергия в поле силы тяжести

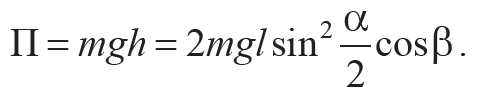
Формула 3.13

При малых углах отклонения, sin(α / 2) ≈ α / 2, изменение потенциальной энергии ΔП диска для двух положений соответствующим углам α_i и α_i+1:

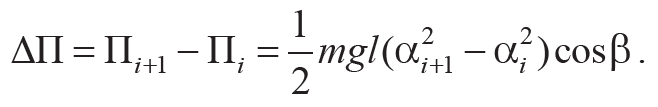
Формула 3.14

Принимая во внимание формулу (3.4) для момента трения качения и учитывая, что сила реакции пластины N = mgsinβ (рис. 3.4, б) и угол поворота диска связан с путем s = (α_i + α_i+1)l, пройденным диском, соотношением ϕ = s / r (рис. 3.4, а), из (3.10) найдем соотношение для работы силы реакции:

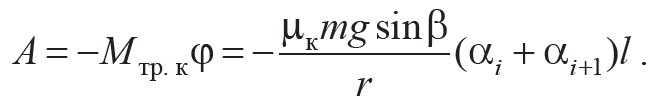
Формула 3.15

Подставляя (3.14) и (3.15) в выражение (3.12), найдем, что два последовательных амплитудных угла отклонения связаны соотношением

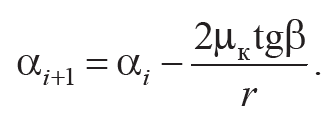
Формула 3.16

Из (3.16) следует, что после n полных колебаний угол отклонения диска n от положения равновесия будет равен

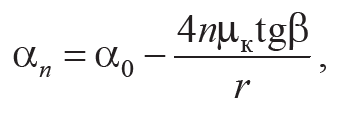
Формула 3.17

где α₀ – начальный угол отклонения.

Отсюда следует расчетная формула для определения коэффициента трения качения:

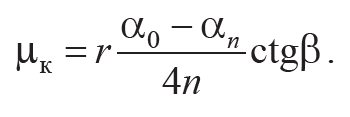
Формула 3.18