



Столкновением (или ударом) называют кратковременное взаимодействие двух или более тел. Заметим, что это понятие относится не только к взаимодействиям, осуществляемым посредством соприкосновения материальных тел. Например, при столкно-вении бильярдных шаров имеет место их контакт. При рассеянии частиц, т. е. при изменении направления движения одних частиц в результате взаимодействия с другими, столкновение происходит без непосредственного контакта.
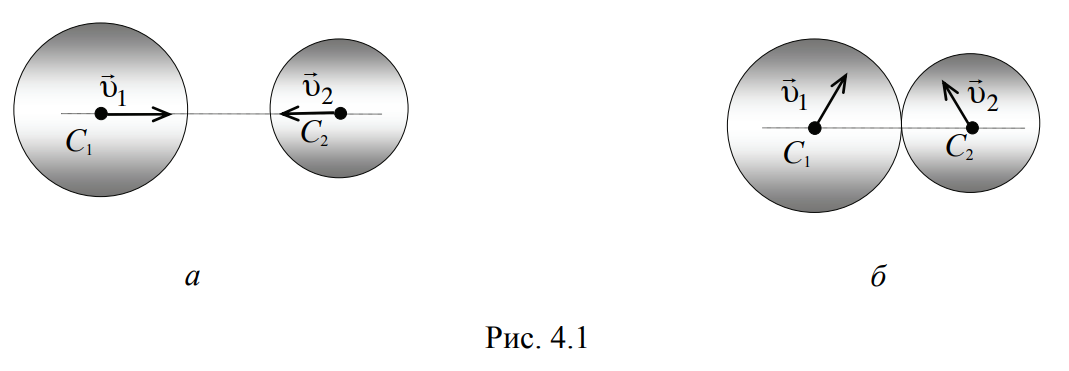
Направления и скорости разлета тел после столкновения зависят от конкретной формы тел и от их взаимной ориентации при ударе. Линией удара называется линия, проходящая через точку касания тел перпендикулярно их поверхностям (пунктирная линия на рис. 4.1). Удар называется центральным, если линия удара проходит через центры масс тел. Например, для шаров удар всегда центральный. Если векторы скоростей тел до удара лежат на линии удара (рис. 4.1, а), то удар называют прямым, в противном случае – прямым, косым (рис. 4.1, б).
Процессы столкновения являются чрезвычайно сложными. Например, в простейшем случае столкновения двух бильярдных шаров: в момент их соприкосновения они испытывают деформа-ции. При этом кинетическая энергия, которой шары обладали пе-ред ударом, частично или полностью переходит в потенциальную энергию деформации тел. Затем энергия деформации снова превращается в кинетическую, однако не полностью – часть энергии превращается во внутреннюю энергию, шары при этом нагреваются. Под внутренней энергией понимают кинетическую энергию и энергию взаимодействия атомов и молекул, из которых состоят тела. Кроме этого, необходимо принять во внимание, что поверхности шаров не являются абсолютно гладкими и между ними возникают силы трения. Эти силы, с одной стороны, также приводят к превращению части энергии во внутреннюю, а с другой – могут вызвать вращение тел.
Между величинами, характеризующими систему до и после столкновения, соблюдаются вполне определенные соотношения, независимые от детального характера взаимодействия. Наличие этих соотношений обусловливается тем, что за время удара действием внешних сил можно пренебречь. Поэтому систему сталкивающих тел можно считать замкнутой, для которой справедливы законы сохранения импульса и энергии.
Согласно закону сохранения импульса, импульс p замкнутой (изолированной) системы, на которую не действуют никакие внешние силы (или их воздействие пренебрежимо мало), сохраняется:
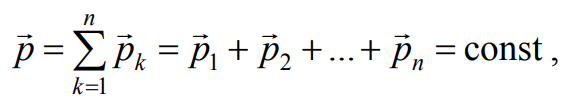
Формула 4.1
где pk=mkυk – импульс отдельного тела в системе.
При применении закона сохранения энергии следует учиты-вать, что кинетическая энергия сталкивающихся тел может пере-ходить во внутреннюю энергию.
Различают три типа столкновения тел: абсолютно неупругое, абсолютно упругое столкновение и промежуточный случай – не-упругое.
Абсолютно неупругое столкновение – это такое столкновение, в результате которого оба тела «слипаются» и далее движутся как единое целое. Кинетическая энергия тел частично или полностью переходит в потенциальную энергию деформации и во внутреннюю энергию тел. Поэтому закон сохранения механической энергии не соблюдается, имеет место закон сохранения суммарной энергии различных видов – механической и внутренней. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, который для двух сталкивающихся тел с массами m1, m2 и скоростями υ1, υ2 имеет вид
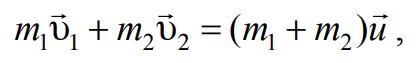
Формула 4.2
где u – скорость центра масс образовавшейся системы.
Абсолютно упругое столкновение – это столкновение тел, при котором их внутренняя энергия не изменяется. Как следствие – не будет изменяться кинетическая энергия системы. Таким образом, при этом виде столкновения выполняются законы сохранения кинетической энергии и импульса, которые для двух сталкивающихся тел имеют вид
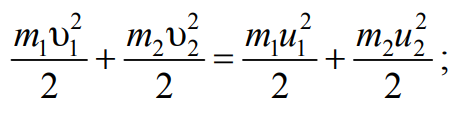
Формула 4.3
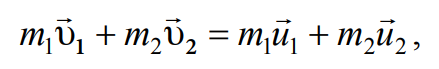
Формула 4.4
где u1 и u2 – скорости тел после удара.
Рассмотрим простейший вариант абсолютно упругого удара – прямой центральный удар двух шаров (рис. 4.1, а), центры масс которых до удара движутся вдоль одной и той же прямой. Скорости тел после удара будут направлены вдоль этой же прямой при таком ударе.
Из закона сохранения кинетической энергии (4.3) следует, что

Формула 4.5
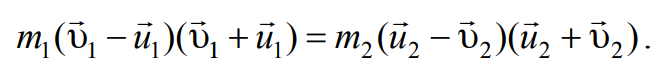
Формула 4.6
Из закона сохранения импульса (4.4) найдем
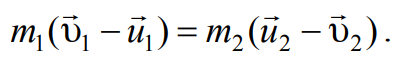
Формула 4.7
Сравнивая (4.6) и (4.7), заключаем, что
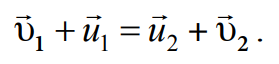
Формула 4.8
Отсюда следует, что относительные скорости шаров до и по-сле столкновения равны по модулю и имеют противоположное направление:
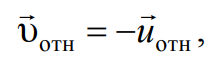
Формула 4.9
где υотн=υ1-υ2, uотн=u1-u2.
Неупругое столкновение – это такое столкновение, в результате которого внутренняя энергия разлетающихся после столкновения тел изменяется, а следовательно, изменяется и суммарная кинетическая энергия системы.
Неупругие столкновения занимают промежуточное положе-ние между абсолютно упругим и абсолютно неупругим столкно-вениями. При абсолютно упругом столкновении, согласно (4.9), модуль относительной скорости тел не изменяется |υотн|=|uотн|. При абсолютно неупругом ударе, поскольку тела после удара не перемещаются относительно друг друга, их относительная ско-рость равна нулю |uотн|=0. При таком ударе модуль относительной скорости изменяется от некоторого, не равного нулю, значения |υотн|≠0 до нуля. В случае неупругих столкновений относительная скорость тел после удара не равна нулю |uотн|≠0 и из-за потерь механической энергии |uотн| <|υотн|. Для характеристики неупругих столкновений вводят коэффициент восстановления скорости kc:
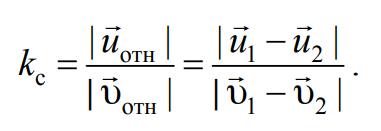
Формула 4.10
Коэффициент восстановления зависит от упругих свойств со-ударяющихся тел и определяет, какая доля начальной относительной скорости этих тел восстанавливается к концу удара. Для абсолютно неупругого столкновения
kc=0, так как |uотн|=0, для абсолютно упругого столкновения
kc=1, так как |υотн|=|uотн|, для неупругих столкновений
0
Для учета потерь механической энергии вводят коэффициент восстановления кинетической энергии kэ:

Формула 4.11
где К и К' – кинетические энергии системы до и после столкновения
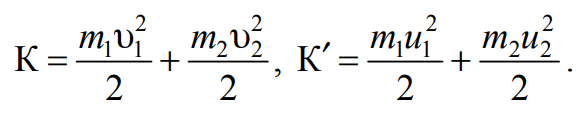
Формула 4.12
При абсолютно упругом столкновении К' = К и kэ=1, при неупругом столкновении kэ<1.
На рис. 4.2, а изображена схема установки для определения скорости шаров до и после их столкновения. Она представляет собой установленный на основании штатив 1, в верхней части которого закреплены бифилярные подвесы (состоящие из двух нитей) 2 длиной l с исследуемыми телами (шарами), навинченными на стержни с указателями, которые служат для отсчета углов отклонения тел по шкалам 3. На установке имеется механизм изменения расстояния между телами, который приводится в действие с помощью винта 4. Правое тело может удерживаться в отклоненном положении с помощью электромагнита 5, который можно перемещать вдоль шкалы и фиксировать в заданном положении. Сквозь подвесы проходят провода, замыкающие электрическую цепь при соприкосновении шаров. Это позволяет по электронному микросекундомеру 6 измерять время взаимодействия шаров при ударе.

Перед началом опыта тела приводят в соприкосновение с по-мощью винта 4. Правый шар отклоняют на некоторый начальный угол αп и фиксируют с помощью электромагнита 5. Затем шар отпускают и по шкалам 3 измеряют углы отклонения левого βл и правого βп шаров сразу после первого соударения (рис. 4.2, б).
Для определения скорости правого тела непосредственно пе-ред ударом воспользуемся законом сохранения механической энергии, пренебрегая сопротивлением воздуха при движении тела. В крайнем правом положении тело обладает потенциальной энергией П=mпghп, а при прохождении положения равновесия непосредственно перед ударом – кинетической энергией R=mпυп2/2. Согласно закону сохранения механической энергии П = К в дан-ном случае. Отсюда найдем скорость правого тела перед ударом:
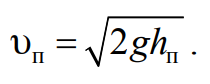
Формула 4.13
Примем во внимание, что при отклонении тела на угол αп от положения равновесия его центр тяжести поднимется на высоту
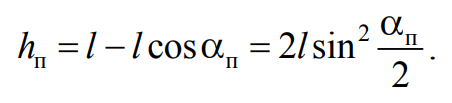
Формула 4.14
Подставив (4.14) в (4.13), найдем
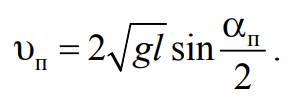
Формула 4.15
Рассуждая аналогичным образом, нетрудно найти скорости тел сразу же после удара:
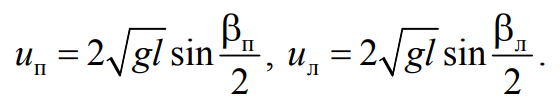
Формула 4.16
Учтем, что углы отклонения тел в данной установке не пре-вышают 8°. Для таких углов sinα≈α относительной ошибкой меньше 0,5%, что значительно меньше случайной и приборной погрешностей определения угла отклонения. Поэтому скорости тел непосредственно до удара и сразу после удара
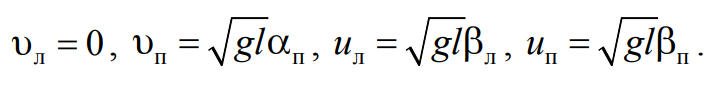
Формула 4.17
Проекции импульсов системы тел на ось х (линию удара) до p1x и после p2x удара имеют вид
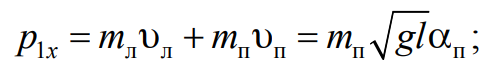
Формула 4.18
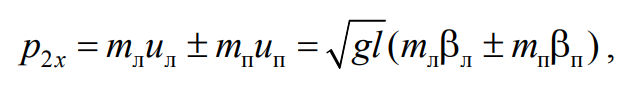
Формула 4.19
где mп, mл – массы правого и левого тел, знаки плюс и минус в (4.19) соответствуют движению правого тела сразу же после удара в положительном направлении оси х и в противоположном направлении соответственно.
Вследствие закона сохранения импульса при столкновении в пределах погрешности измерения должно удовлетворяться приближенное равенство p1x≈p2x. Погрешность измерения импульса системы p2x связана с погрешностями измерения углов отклонения тел βл и βп. Используя формулу (1.10), погрешность косвенного измерения импульса системы p2x определяется соотношением
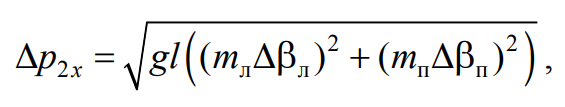
Формула 4.20
где Δβл и Δβп – погрешности измерения углов.
Учитывая в (4.10) направления скоростей тел до и после удара и формулы для их модулей (4.17), найдем коэффициент восстановления скорости:
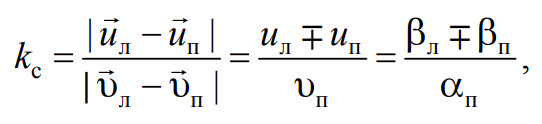
Формула 4.21
где знаки минус и плюс соответствуют движению правого тела сразу же после удара в положительном направлении оси х и в противоположном направлении соответственно.
С учетом (4.17) коэффициент восстановления кинетической энергии (4.11) примет вид
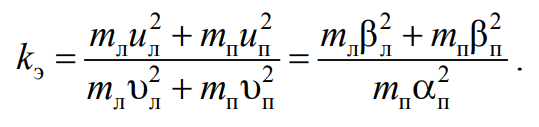
Формула 4.22
При ударе левое тело изменит свой импульс на величину Δp=mлuл. По второму закону Ньютона среднее значение силы, действующей на левое тело, определяется соотношением
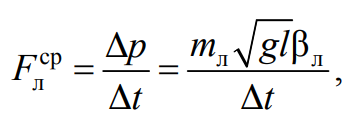
Формула 4.23
где Δt – время взаимодействия тел.
1. Подготовьте таблицу для внесения и обработки результатов измерений.
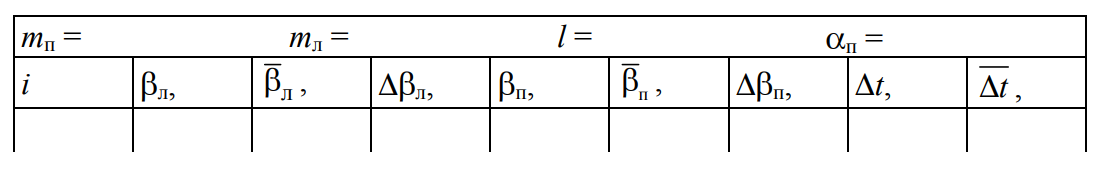
2. Занесите в таблицу массы шаров и длину бифилярного подвеса (указаны на установке). С помощью винта 4 приведите шары в соприкосновение. Убедитесь, что точка касания лежит на линии, проходящей через центры шаров. Отрегулируйте положение левой шкалы 3 так, чтобы указатель левого шара был совмещен с ее нулем.
3. Подключите шнур питания установки к электрической сети, нажмите кнопку «СЕТЬ» и отпустите кнопку «ПУСК». Отклоните правый шар так, чтобы он притянулся к электромагниту 5. Отпустите стопорный винт электромагнита, а затем переместите и закрепите электромагнит так, чтобы угол отклонения шара соответствовал α=5°-8°. Значение угла занесите в таблицу.
4. Нажав кнопку «ПУСК», выключите электромагнит. Сразу же после столкновения шаров определите максимальный угол отклонения левого βл и правого βп шаров. Обратите внимание на направления движения правого шара сразу после удара. Снимите показания секундомера Δt. Затем нажмите кнопку «СБРОС» для обнуления показаний секундомера.
5. Повторите измерения углов βл, βп и времени соударения Δt еще не менее чем в пяти столкновениях при одном и том же на-чальном угле отклонения α=п правого шара. Результаты измерений занесите в таблицу.
6. Определите средние значения углов $$\overline{β_л}$$, $$\overline{β_п}$$, и времени $$\overline{Δt}$$. По формуле (О7) вычислите полные погрешности прямых измерений углов Δβл и Δβп, где случайные погрешности $$Δβ_п{^{сл}}, Δβ_п{^{сл}}$$ вычисляются по формулам (О4), (О5) соответственно.
7. Используя значения углов αп, $$\overline{β_л}$$, $$\overline{β_п}$$, выраженные в радианах, по формулам (4.18), (4.19) вычислите проекции импульсов системы тел на линию удара до p1x и после p2x столкновения.
8. Используя значения погрешностей углов Δβл, Δβп, выраженных в радианах, по формуле (4.20) вычислите погрешность Δp2x косвенного измерения импульса системы p2x.
9. Используя значения углов αп, $$\overline{β_л}$$, $$\overline{β_п}$$, по формулам (4.21), (4.22) определите коэффициенты восстановления скорости и кинетической энергии.
10. Используя значение $$\overline{β_л}$$, выраженное в радианах, и среднее значение времени удара $$\overline{Δt}$$, по формуле (4.23) вычислите среднее значение силы, действующей на левое тело.
11. Подготовьте выводы по выполненной лабораторной работе.