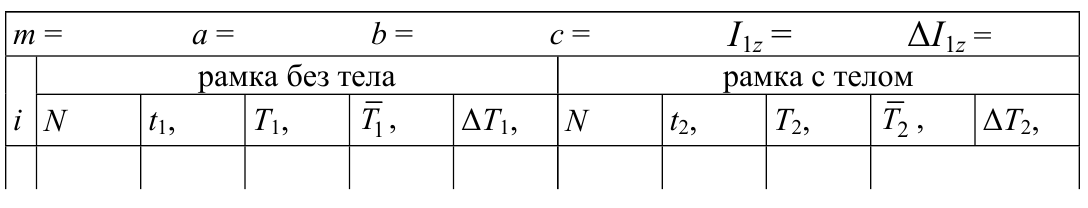Моментом инерции I_z системы материальных точек относительно оси z называют физическую величину, равную сумме произведений масс материальных точек mi на квадраты расстояний их до оси вращения r_i:

Формула 5.1

Формула для момента инерции абсолютно твердого тела следует из (5.1), если рассматривать тело как систему частиц (материальных точек) с неизменным расстоянием между ними (рис. 5.1). Заменяя в (5.1) массу материальной точки m_i на массу dm =ρdV элементарного объема dV тела и переходя от суммирования к интегрированию по объему V тела, получим формулу, которую используют для вычисления момента инерции абсолютно твердого тела

Формула 5.2

где ρ – плотность материала тела.

Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения, т. е. является мерой инертности при вращательном движении. Напомним, что инертность – это способность тел препятствовать изменению своей скорости относительно инерциальной системы отсчета при воздействии на него внешних сил. Таким образом, чем больший момент инерции относительно некоторой оси имеет тело, тем труднее раскрутить это тело относительно данной оси.

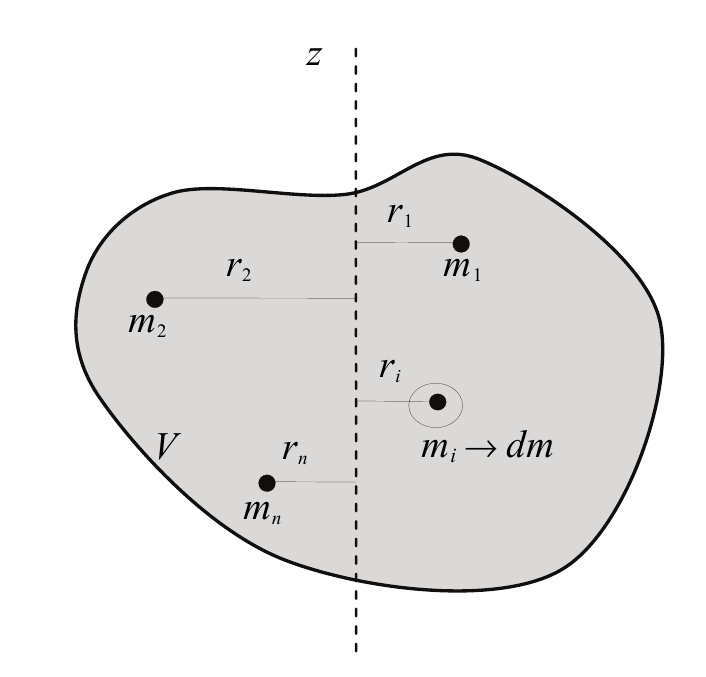
Рисунок 5.1

Момент инерции тела зависит от распределения масс относительно данной оси. Если вычислить сумму (5.1) или интеграл (5.2), то момент инерции любого тела можно выразить через массу тела, его геометрические размеры и положение относительно оси вращения. Во многих случаях расчеты существенно упрощаются при использовании двух свойств момента инерции, которые следуют из определения (5.1) этой величины – аддитивность момента инерции и теорема Штейнера.

Аддитивность (от англ. to add – добавлять, суммировать) момента инерции означает, что момент инерции системы относительно некоторой оси равен сумме моментов инерции тел или всех частей системы относительно этой оси. В случае непрерывно распределенной массы (твердого тела) сумма переходит в интеграл

Формула 5.3

где I_kz – моменты инерции тел, входящих в систему $$(k=\overline{1,n})$$; dI_z – момент инерции малого элемента объема тела dV .

По теореме Штейнера момент инерции I_z тела относительно произвольной оси z равен сумме момента инерции I'_Сz относительно оси z', параллельной данной и проходящей через центр масс C тела, и произведения массы тела m на квадрат расстояния d между осями (рис. 5.2):

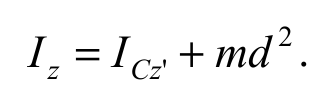
Формула 5.4

Эта теорема сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела.

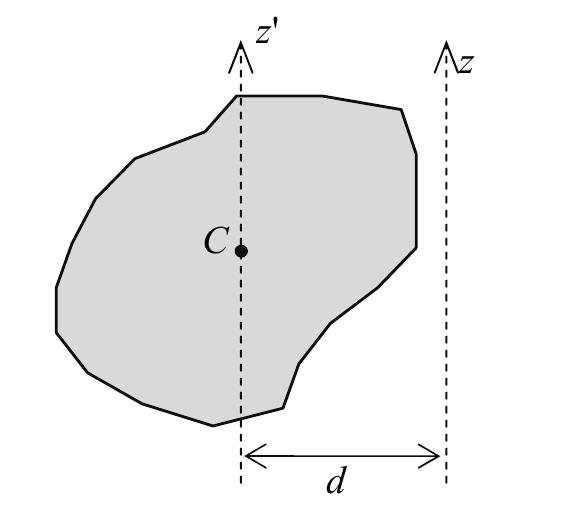
Рисунок 5.2

Рассмотрим несколько примеров вычисления моментов инерции тел, имеющих простую форму.

1. Момент инерции однородного тонкого стержня. Определим момент инерции однородного стержня длиной l относительно оси z, перпендикулярной стержню и проходящей через его центр масс С (рис. 5.3, а.)

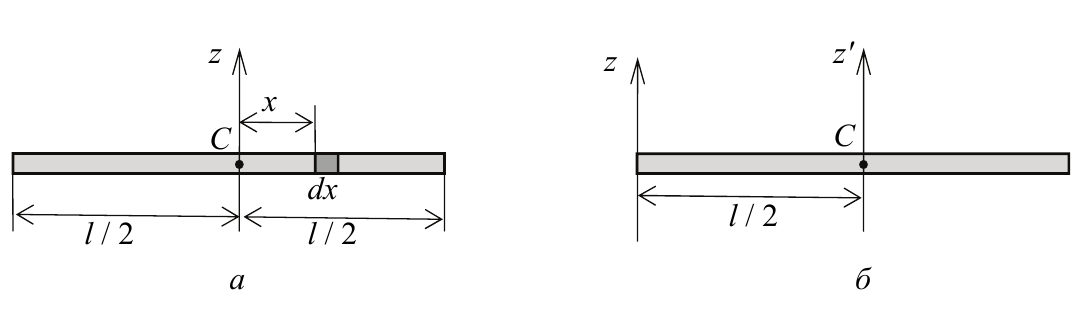
Рисунок 5.3

Разделим стержень на бесконечно малые элементы длиной dx. Объем элемента dV = Sdx, где S – площадь поперечного сечения стержня. Момент инерции элемента, расположенного на расстоянии x от оси, определяется соотношением

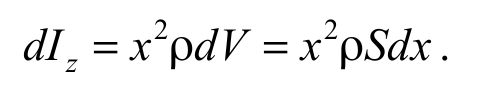
Формула 5.5

Согласно (5.2) момент инерции стержня

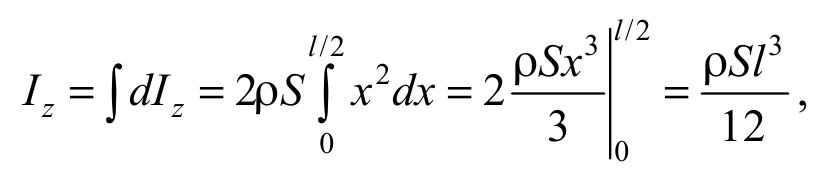
Формула 5.6

где множитель 2 учитывает две половины стержня, расположенные симметрично относительно оси z.

Так как масса стержня m=ρV=ρSl, получим

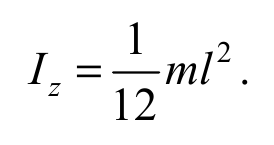
Формула 5.7

Момент инерции стержня относительно оси, проходящей через один из его концов (рис. 5.3, б), найдем, воспользовавшись теоремой Штейнера (5.4). Учитывая момент инерции стержня относительно центра масс (5.7) и расстояние между осями d = l / 2, получим

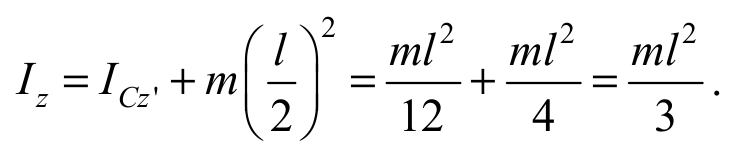
Формула 5.8

2. Момент инерции параллелепипеда. Определим момент инерции параллелепипеда относительно оси z, проходящей через его центр масс перпендикулярно боковым граням (рис. 5.4). Через a, b, c обозначим боковые ребра параллелепипеда.

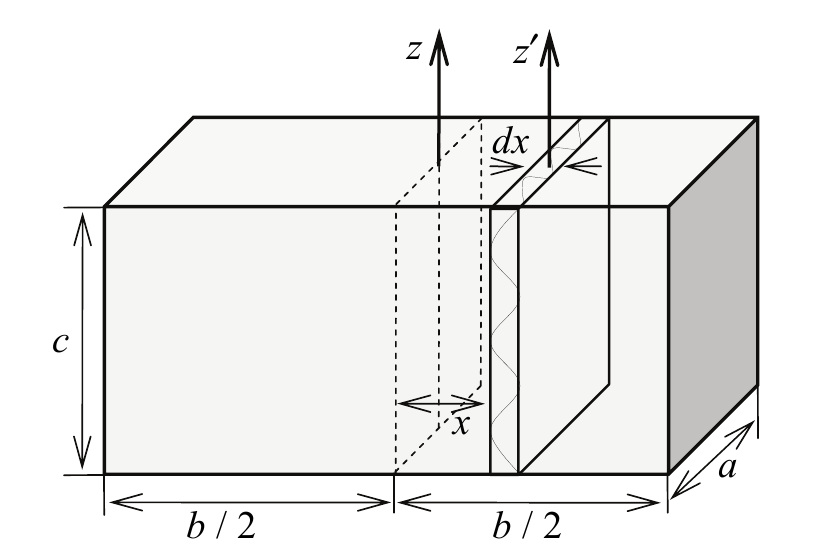
Рисунок 5.4

Разделим параллелепипед на тонкие пластины толщиной dx, параллельные одной из граней параллелепипеда. Они имеют объем dV = aсdx и массу dm = ρdV = ρaсdx. Пластину можно считать совокупностью параллельных полосок (стержней) длиной а, поэтому ее момент инерции относительно оси z′, проходящей через центр масс пластины параллельно оси z, определяется соотношением (5.7):

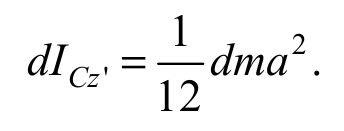
Формула 5.9

Момент инерции пластины относительно оси z, расположенной на расстоянии x от нее, найдем по теореме Штейнера (5.4):

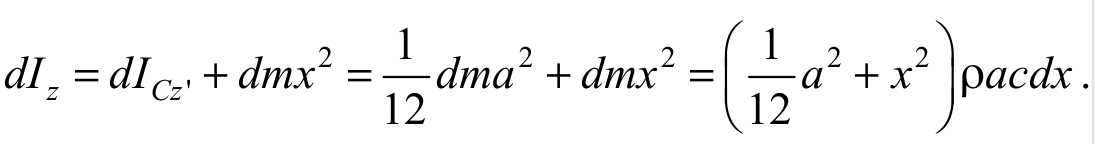
Формула 5.10

Принимая во внимание, что расстояние x для разных пластин изменяется от 0 до b / 2, по формуле (5.2) найдем момент инерции параллелепипеда:

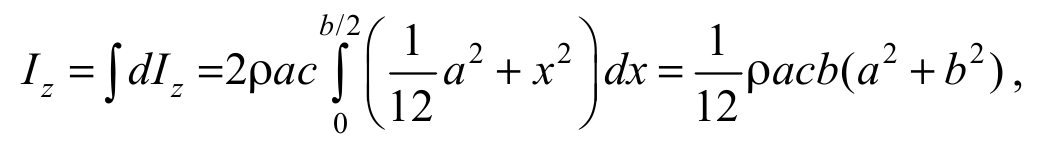
Формула 5.11

где учтены две половины параллелепипеда, расположенные симметрично относительно оси z.

Учитывая в (5.11), что V = acb – объем параллелепипеда и m = ρV – его масса, окончательно получим

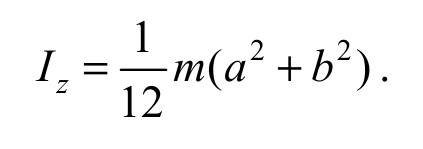
Формула 5.12

Если тело имеет сложную геометрическую форму или распределение плотности по объему неизвестно, то вычисление моментов инерции оказывается затруднительным либо невозможным.В этом случае целесообразно использовать экспериментальные методы. В данной работе для определения момента инерции тела I_z применяется крутильный маятник, показанный на рис. 5.5. Исследуемое тело 1 закрепляется с помощью подвижной балки 2 на рамке 3, подвешенной на стальной вертикальной проволоке 4, натянутой между двумя кронштейнами 5, жестко соединенными со стойкой 6 установки. За рамкой имеется электромагнит 7, который фиксирует ее в отклоненном на угол φ₀ положении. Угол отклонения определяется по шкале 8. Подсчет числа N колебаний рамки осуществляет электронная система, основными деталями которой являются фотоэлектрический датчик 9, который соединен с цифровым счетчиком числа колебаний и секундомером 10.

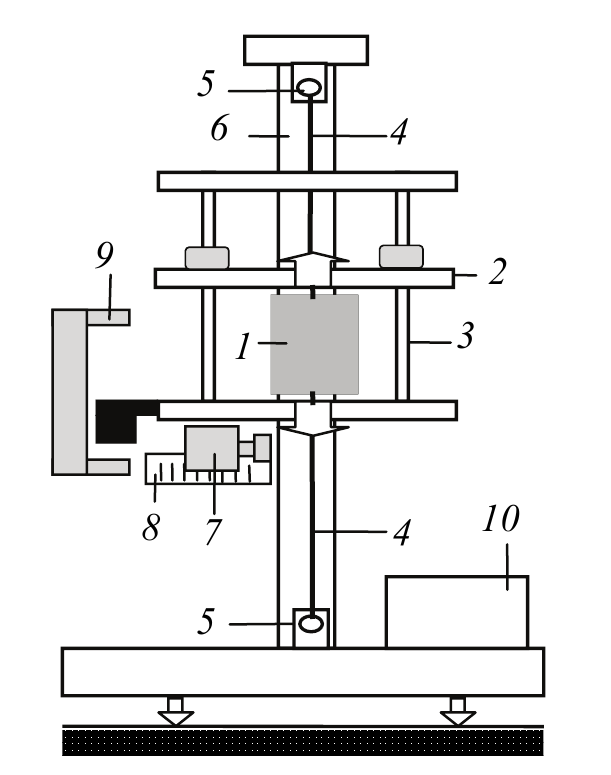
Рисунок 5.5

Под действием сил упругости закрученной на угол φ проволоки рамка совершает крутильные колебания. Согласно закону Гука момент сил упругости, действующий на рамку

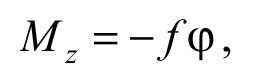
Формула 5.13

где ƒ – коэффициент крутильной жесткости проволоки, который называют модулем кручения.

Угловое ускорение рамки ε = d²φ / dt² определяется основным уравнением динамики вращательного движения:

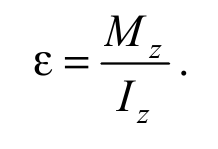
Формула 5.14

Пренебрегая сопротивлением воздуха и учитывая (5.13), из этого уравнения следует дифференциальное уравнение колебаний рамки

Формула 5.15

где ω₀ – циклическая частота колебаний рамки.

Решение уравнения (5.15) имеет вид гармонических колебаний:

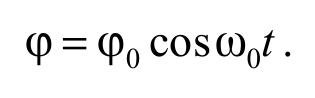
Формула 5.16

Из (5.16) следует, что период колебаний рамки определяется соотношением

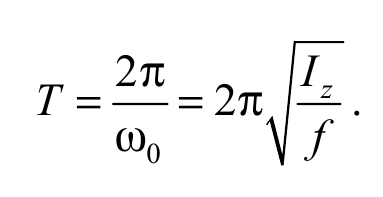
Формула 5.17

Измеряя на эксперименте период колебаний T₁ рамки и период колебаний T₂ рамки с закрепленным на ней телом, получим систему двух уравнений

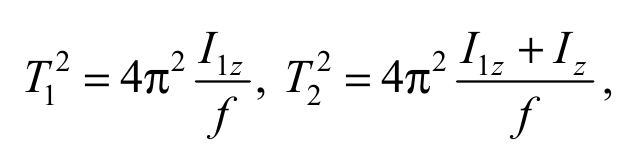
Формула 5.18

где I_1z – момент инерции рамки; I_z – момент инерции исследуемого тела.

Отсюда следует, что

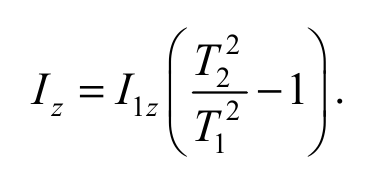
Формула 5.19

Погрешность косвенного измерения момента инерции I_z по формуле (5.19) определяется погрешностями момента инерции рамки ΔI_1z и периодов колебаний ΔT₁, ΔT₂. Соотношения для расчета относительной ε и абсолютной ΔI_z погрешностей следуют из (О10):

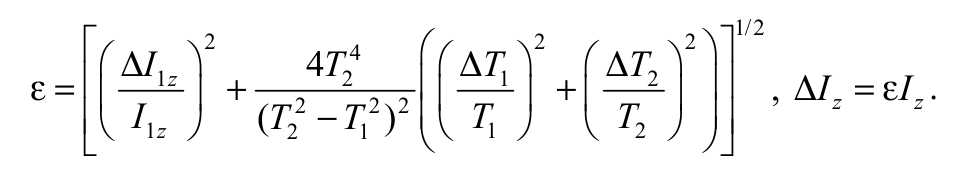
Формула 5.20