



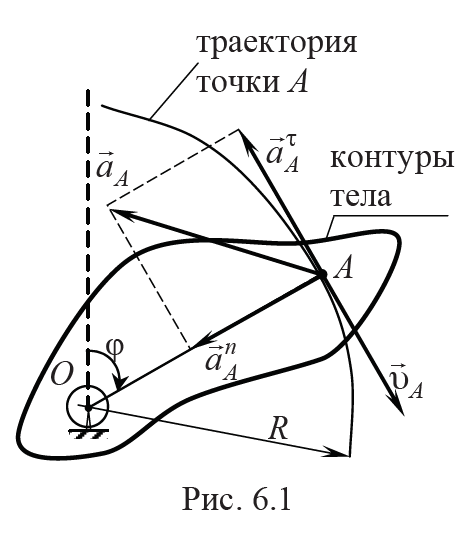
Кинематическое уравнение вращательного движения твердого тела относительно неподвижной оси определяет зависимость угла поворота φ тела от времени t (рис. 6.1, ось вращения проходит через точку О перпендикулярно плоскости рисунка)
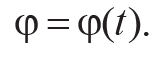
Формула 6.1
Угловая скорость ω тела определяет быстроту изменения угла поворота и численно равна первой производной от угла поворота φ по времени t:
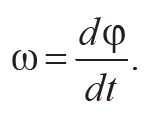
Формула 6.2
Угловое ускорение ε тела определяет быстроту изменения угловой скорости и, следовательно, оно численно равно первой производной от угловой скорости ω по времени t либо второй производной от угла поворота φ по времени t:
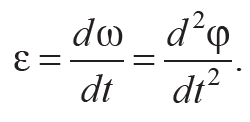
Формула 6.3
Угловые скорость и ускорение тела позволяют определить скорость υ и ускорение a любой точки этого тела, например точки А, движущейся по окружности радиуса R = OA:
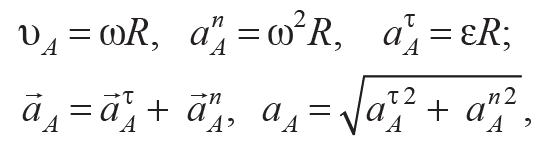
Формула 6.4
где $$a^τ_A$$ и $$a^n_A$$ – касательное и нормальное ускорения точки А.
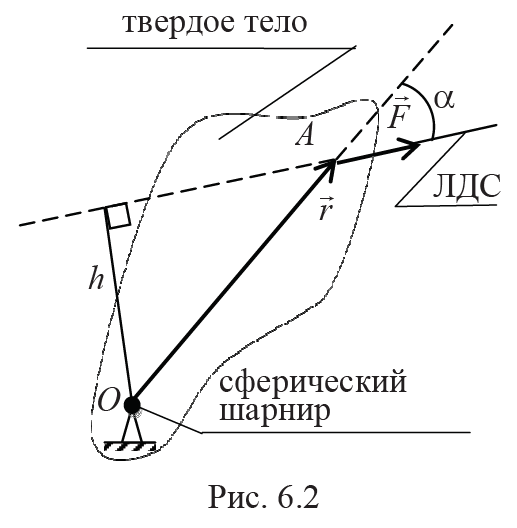
Момент силы F относительно точки О (рис. 6.2) определяет способность силы F вызвать вращение тела вокруг этой точки. Он равен векторному произведению радиус-вектора r точки А приложения силы F на вектор силы:
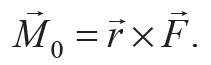
Формула 6.5
Модуль момента силы
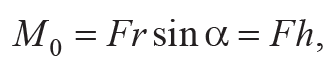
Формула 6.6
где h = rsinα – плечо силы F, т. е. кратчайшее расстояние от точки О до линии действия силы F (ЛДС). Направление вектора M0 находится по правилу векторного произведения, которое согласуется с правилом правой руки, или правилом буравчика.
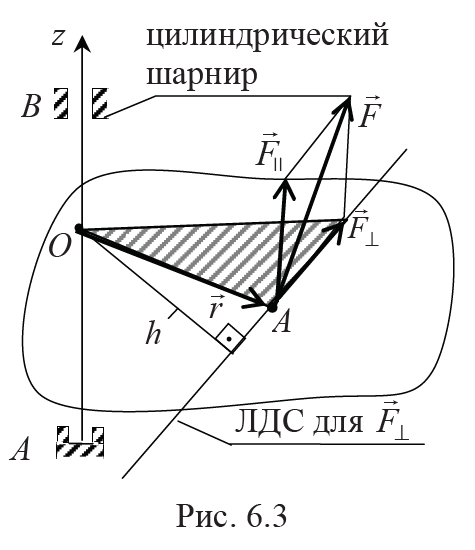
Момент силы F относительно оси z равен моменту ее перпендикулярной к оси составляющей F⊥ относительно точки О, находящейсяся на оси z (рис. 6.3):
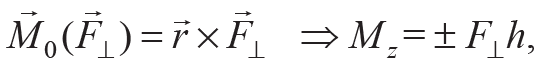
Формула 6.7
где h – плечо силы F⊥ относительно точки О (заштрихованный треугольник расположен в горизонтальной плоскости); Mz – алгебраическое значение момента силы относительно оси z, которое равно проекции вектора М0 на эту ось. Отсюда следует правило знаков для Mz: если, наблюдая с конца оси z, поворот под действием силы F⊥ происходит против часовой стрелки (как на рис. 6.3), то момент Mz считается положительным, иначе – отрицательным.
В частном случае, если сила F параллельна оси z, то ее перпендикулярная проекция F⊥ = 0 и, следовательно, момент силы F относительно этой оси равен нулю.
Моментом инерции Iz тела относительно оси z называют величину (см. лаб. раб. № 5)
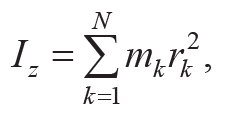
Формула 6.8
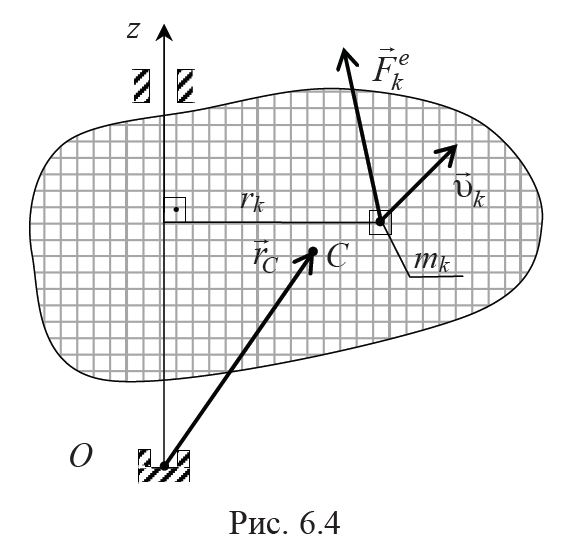
где mk – массы частиц, на которые мысленно можно разбить тело, а rk – расстояния от этих масс до оси z (рис. 6.4).
Основное уравнение динамики вращательного движения, описывающее вращение твердого тела относительно неподвижной оси, имеет следующий вид:
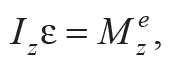
Формула 6.9
где$$M^e_z$$ – суммарный момент внешних сил, действующих на тело.
Уравнение (6.9) можно рассматривать как аналог 2-го закона Ньютона для материальной точки, или уравнения, описывающего движение центра масс твердого тела, или, в частности, поступательного движения этого тела:
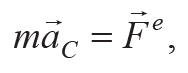
Формула 6.10
где m – масса тела; aC – ускорение центра масс C тела; Fe – суммарная внешняя сила, действующая на тело.
Радиус-вектор центра масс (точки C) определяется соотношением
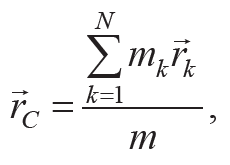
Формула 6.11
где rk – радиус-векторы частиц, на которые мысленно можно разбить тело массой m.
Из сопоставления (6.9) и (6.10) следует, что, поскольку масса m во 2-м законе Ньютона является мерой инертности материальной точки, то момент инерции Iz является мерой инертности для вращательного движения тела.
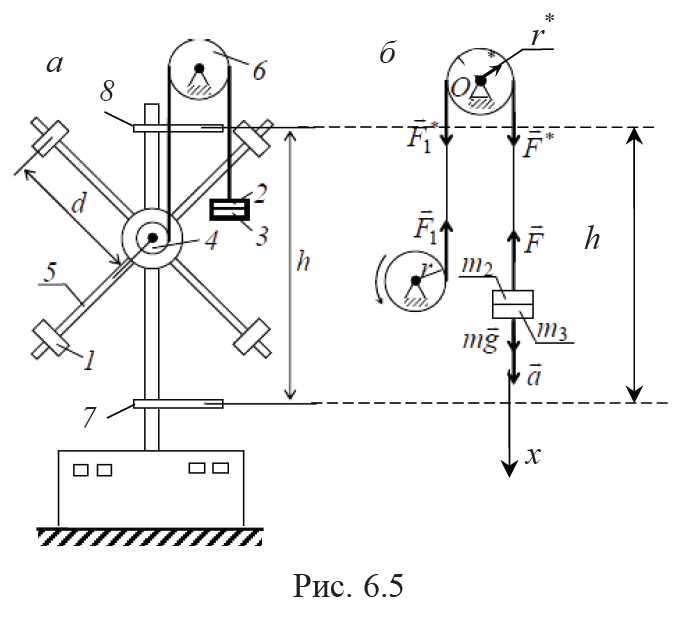
Общий вид маятника Обербека изображен на рис. 6.5, a. На вертикальной стойке имеется подшипниковый узел, на котором укреплен двухступенчатый блок 4 с четырьмя стержнями 5, образующими крестовину. На стержнях 5 крестовины выполнены кольцевые выточки через 1 см друг от друга, первая из которых находится на расстоянии d1 = 4 см от оси вращения, а последняя – на расстоянии 25 см. Они позволяют закрепить четыре передвижных груза 1 на заданном расстоянии d от оси вращения. На одну из ступеней блока 4 наматывается нить, перекинутая через блок 6, к ее концу прикреплена нагрузочная площадка 3. На стойке имеются нижний неподвижный 7 и верхний подвижный 8 кронштейны с фотоэлектрическими датчиками. Для измерения высоты h между датчиками на стойке нанесена миллиметровая шкала. При утопленной кнопке «ПУСК» и нажатой кнопке «СЕТЬ» нить наматывают на блок 4 до тех пор, пока нижняя плоскость площадки 3 с грузами 2 не окажется немного выше риски, нанесенной на верхнем кронштейне, т. е. выше светового луча фотоэлектрического датчика. После этого кнопка «ПУСК» отпускается, а тормозной электромагнит прижимает фрикционную муфту и удерживает маятник вместе с грузами в состоянии покоя. Следующее нажатие кнопки «ПУСК» освобождает маятник, и он начинает вращаться под действием нагруженной площадки 3. При пересечении площадкой 3 светового луча верхний фотоэлектрический датчик включает секундомер, шкала которого установлена на передней панели основания прибора. Площадка с грузами совершает поступательное, а маятник – вращательное движения. При пересечении площадкой светового луча нижнего фотоэлектрического датчика на кронштейне 7 автоматически выключается секундомер и включается тормозной электромагнит.
Пренебрегая сопротивлением воздуха и трением в подшипнике, можно воспользоваться формулами равноускоренного движения маятника из состояния покоя и получить формулу для косвенного измерения углового ускорения ε блока 4 с крестовиной:
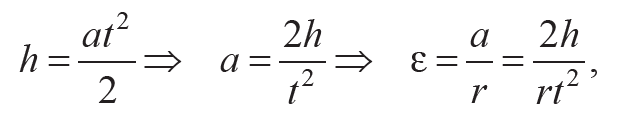
Формула 6.12
где r – радиус использованной ступени блока 4; а – ускорение площадки 3; t – время, отсчитанное секундомером.
Проведем динамическое (теоретическое) исследование движения маятника Обербека, используя его схему (рис. 6.5, б), на которой крестовина не изображена. Воспользуемся 2-м законом Ньютона для площадки с грузами массой m = m2 + m3 (в проекции на направление движения) и основным уравнением динамики вращательного движения для блока 4 с крестовиной и грузами 1. Снова пренебрегая сопротивлением воздуха и трением в подшипнике, получим систему двух уравнений:
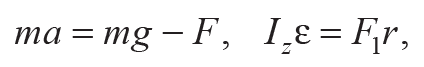
Формула 6.13
где Iz – момент инерции крестовины с грузами; F и F1 – силы натяжения правого и левого вертикальных участков нити.
Основное уравнение динамики для вращательного движения блока 6 имеет вид $$I^*_zε=(F^*−F^*_1)r^*$$. Инерционные свойства этого блока весьма малы по сравнению с крестовиной, т. е. $$I^*_z << I_z$$, что позволяет считать осевой момент инерции $$I^*_z ≈ 0$$ а значит, $$F^*≈F^*_1$$. Согласно 3-му закону Ньютона $$F = F^*$$ и $$F_1 = F^*_1$$. Следовательно, $$F_1 = F$$ , что позволяет исключить неизвестную силу натяжения нити из системы (6.13). Принимая во внимание кинематическое соотношение a = εr, можно получить теоретическое выражение для углового ускорения ε блока 4 с крестовиной (решите систему (6.13) и получите выражение для ε(т) самостоятельно):
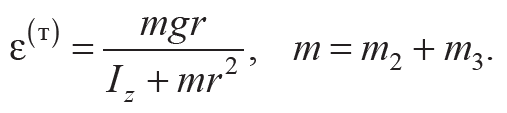
Формула 6.14
1. Подготовьте таблицу для занесения и обработки результатов измерений.
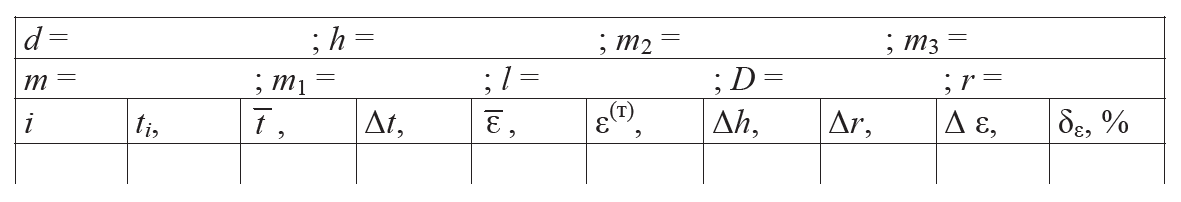
2. В соответствии с номером звена в подгруппе определите расстояние d по формуле d = 0,11 + 0,02m и расстояние h = 0,41 + + 0,01m (в метрах, m – номер Вашего звена в подгруппе). Если номер звена в подгруппе нечетный, то используется груз массой m2 = 43 г, если четный, то m2 = 84 г.
3. Закрепите передвижные грузы 1 массой m1 (массы указаны на самих грузах) на четырех стержнях крестовины на расстоянии d. Штангенциркулем измерьте размеры груза 1 (его толщину l и диаметр D = 2R), а также радиус r используемой ступени блока 4.
4. Небольшими смещениями грузов 1 отцентрируйте маятник для двух взаимно перпендикулярных положений крестовины. Если центровка выполнена правильно, то маятник при отсутствии натяжения нити при любой ориентации будет находиться в равновесии (безразличное равновесие).
5. Зафиксируйте верхний передвижной кронштейн 8 на заданной высоте h так, чтобы его верхняя плоскость совпадала с соответствующим делением шкалы на стойке. Вставьте вилку кабеля питания установки в розетку электрической сети.
6. Положите на нагрузочную площадку 3 массой m3 заданный груз массой m2, тогда масса, создающая ускорение, будет равна m = m2 + m3 (значение m3 указано на площадке). Закрепите конец нити на ступени радиусом r блока 4. Утопите кнопку «ПУСК» и нажмите кнопку «СЕТЬ».
7. Вращая маятник, наматывайте нить на выбранную ступень диска до тех пор, пока нижняя плоскость нагрузочной площадки 3 не поднимется чуть выше линии, нанесенной на верхнем кронштейне. Отпустите кнопку «ПУСК», при этом электромагнит прижмет фрикционную муфту и будет удерживать крестовину в состоянии покоя.
8. Нажмите кнопку «СБРОС» и утопите кнопку «ПУСК». Как только площадка 3 начнет двигаться, она закроет световой луч и верхний фотодатчик запустит секундомер . Он остановится в тот момент, когда площадка закроет световой луч нижнего фотодатчика. Значение t1 занесите в таблицу. Нажмите кнопку «СБРОС». Пункты 7, 8 опыта повторите еще 5 раз (i = 2, …, 6).
9. Рассчитайте среднее значение времени tсред, затем, используя tсред, по формуле (6.12) вычислите среднее угловое ускорение εсред.
10. В соответствии с методикой прямых измерений определите приборные погрешности Δr, Δh и случайную погрешность Δt при доверительной вероятности р = 0,95. Самостоятельно выведите формулу для относительной погрешности δε косвенного измерения углового ускорения (с помощью формулы (6.12)), которая имеет следующий вид:
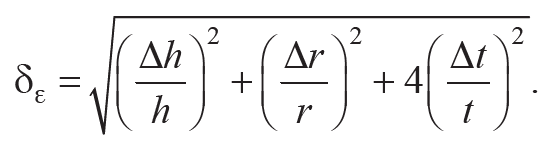
Формула 6.15
Вычислите относительную δε и абсолютную Δε погрешности (Δε = δεεcред).
11. По формуле (6.14) рассчитайте теоретическое ускорение ε(т). Учтите, что момент инерции маятника Iz = I0 + 4I1, где I0 = 4,71 × 10–3 кг·м2 – момент инерции крестовины без грузов, а момент инерции I1 груза 1 на расстоянии d от оси вращения вычисляйте как для материальной точки (I1 = m1d2).
12. Рассчитайте значение момента инерции $$I^*_1$$ груза 1 как для цилиндра радиусом R = D / 2 и высотой l, используя формулу
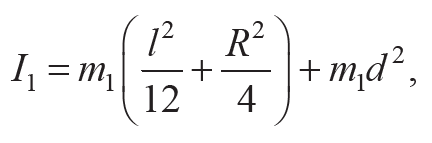
Формула 6.16
которая получена с помощью теоремы Штейнера. Рассчитайте уточненные значения Iz и ε(т).
13. Подготовьте выводы по выполненной лабораторной работе.